§ 19. Напружанасць электрастатычнага поля. Прынцып суперпазіцыі

Для вывучэння ўласцівасцей электрастатычнага поля зручна вы ка рыстоў ваць такую яго характарыстыку, якая не залежыць ад лікавага зна чэння пробнага зараду і дазваляе вызначыць сілу, што дзейнічае на зарад з боку поля ў любым яго пункце. Для гравітацый нага поля характарыстыкай, якая не залежыць ад масы цела, з’яўляецца паскарэнне свабоднага падзення $g with rightwards arrow on top equals fraction numerator F with rightwards arrow on top over denominator m end fraction$ . А якая фізічная велічыня з’яўляецца ха рак тарыстыкай электрастатычнага поля?

Напружанасць электрастатычнага поля. Няхай электрастатычнае поле створана ў вакууме пунктавым зарадам Q > 0. Калі ў пэўны пункт поля змясціць пробны дадатны зарад q₀, на яго будзе дзейнічаць кулонаўская сіла адштурхвання, модуль якой $F equals k fraction numerator Q q subscript 0 over denominator r squared end fraction$ .

Сіла $F with rightwards arrow on top$ не можа з’яўляцца характарыстыкай поля, бо яе модуль прапарцыянальны значэнню пробнага зараду q₀. Аднак адносіны модуля сілы, якой электрастатычнае поле пунктавага зараду Q дзейнічае на пробны зарад q₀, не залежаць ад значэння пробнага зараду:

$F over q subscript 0 equals k Q over r squared$ ,

(19.1)

а значыць, могуць служыць характарыстыкай поля.

Гэтая характарыстыка атрымала назву напружанасць электрастатычнага поля і яе абазначаюць $E with rightwards arrow on top$ . Напружанасць характарызуе сілавое дзеянне поля на ўнесеныя ў яго зарады.

Напружанасць электрастатычнага поля — фізічная вектарная велічыня, роўная адносінам сілы, якой поле дзейнічае на пробны зарад, да значэння гэтага зараду:

$E with rightwards arrow on top equals fraction numerator F with rightwards arrow on top over denominator q subscript 0 end fraction.$

(19.2)

З улікам выразаў (19.1) і (19.2) можна вызначыць модуль напружанасці элек тра статычнага поля, створанага пунктавым зарадам Q, у пункце, які зна ходзіц ца на адлегласці r ад яго:

$E equals k fraction numerator open vertical bar Q close vertical bar over denominator r squared end fraction.$

Такім чынам, модуль напружанасці поля, стваранага ў вакууме пунктавым зарадам, прама прапарцыянальны модулю гэтага зараду і адваротна прапарцыянальны квадрату адлегласці паміж зарадам і пунктам, у якім вызначаюць значэнне напружанасці.

Калі зарад Q знаходзіцца ў аднародным асяроддзі з дыэлектрычнай пранікаль насцю ε, то модуль напружанасці поля $E equals k fraction numerator open vertical bar Q close vertical bar over denominator straight epsilon r squared end fraction$ .

З выразу $E with rightwards arrow on top equals fraction numerator F with rightwards arrow on top over denominator q subscript 0 end fraction$ вынікае, што адзінкай напружанасці электрастатычнага поля ў СІ з’яўляецца ньютан на кулон $open parentheses straight Н over Кл close parentheses$ . Аднак у СІ шырока выкарыстоў ваюць іншую назву гэтай адзінкі — вольт на метр $open parentheses straight В over straight м close parentheses$ .

Ведаючы напружанасць электрастатычнага поля, можна вызначыць сілу, якая дзейнічае на любы пунктавы зарад у любым пункце гэтага поля:

$F with rightwards arrow on top equals E with rightwards arrow on top q.$

(19.3)

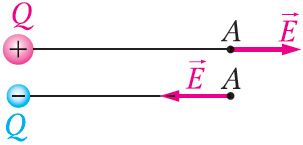
Напружанасць поля, як і сіла, велічыня вектарная. Напрамак напружанасці поля супадае з напрамкам сілы, якая дзейнічае на дадатны пробны электрычны зарад. Напружанасць у любым пункце электрастатычнага поля пунктавага зараду накіравана ўздоўж прамой, што злучае гэты пункт і пунктавы зарад, які стварае поле. Напружанасць поля, створанага пунктавым дадатным зарадам Q > 0, накіравана ад зараду, а напружанасць поля, створанага пунктавым адмоўным зарадам Q < 0, — да зараду (мал. 104).

Ад тэорыі да практыкі

1. Як зменіцца модуль напружанасці ў некаторым пункце поля, створанага пунктавым зарадам Q, калі: а) адлегласць r ад зараду да гэтага пункта павялічыць удвая; б) зарад Q павялічыць удвая, а адлегласць r ад зараду да гэтага пункта паменшыць удвая?

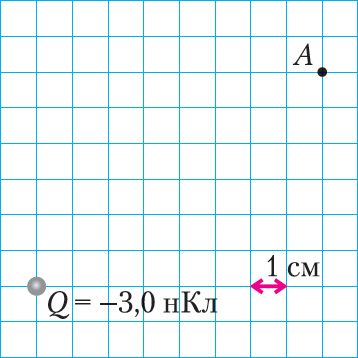
2. Як накіравана ў пункце А напружанасць поля, створанага нерухомым пунктавым зарадам (мал. 105)? Чаму роўны модуль напружанасці поля ў гэтым пункце?

Адсылка да электроннага дадатку для павышанага ўзроўню

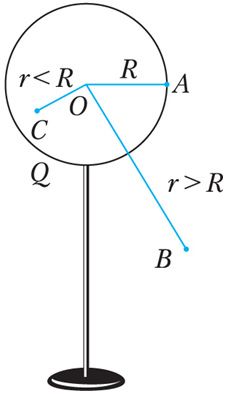
Модуль напружанасці поля адасобленай праводнай сферы радыусам R, зарад якой Q (мал. 105.1), у пунктах на яе паверхні r = R і за сферай на адлегласці r = R ад яе цэнтра вызначаюць па формуле $E equals k fraction numerator open vertical bar Q close vertical bar over denominator r squared end fraction$ . У пунктах, якія знаходзяцца ўнутры праводнай сферы r < R, напружанасць роўная нулю $E with rightwards arrow on top equals 0 with rightwards arrow on top$ , калі ўнутры гэтай сферы няма электрычных зарадаў.

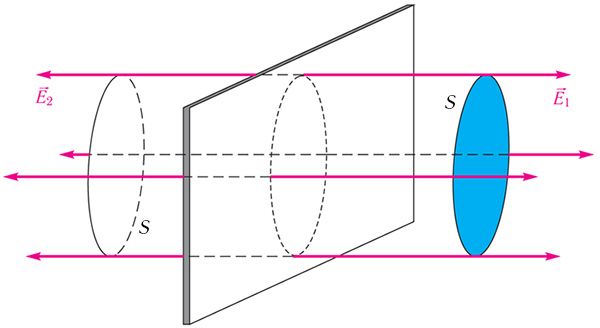
Напружанасць электрастатычнага поля, створанага раўнамерна зараджанай бясконцай плоскасцю, аднолькавая ва ўсіх пунктах паўпрасторы з кожнага боку ад плоскасці (пры гэтым $E with rightwards arrow on top subscript 1 equals negative E with rightwards arrow on top subscript 2$ ), а яе модуль

$open vertical bar E with rightwards arrow on top subscript 1 close vertical bar equals open vertical bar E with rightwards arrow on top subscript 2 close vertical bar equals E equals fraction numerator Q over denominator 2 straight epsilon subscript 0 S end fraction comma$

дзе S — плошча некаторага ўчастка плоскасці, $open vertical bar Q close vertical bar$ — модуль зараду гэтага ўчастка (мал. 105.2).

Цікава ведаць

Акрамя гравітацыйнага поля, у Зямлі ёсць электрычнае і магнітнае палі. Модуль напружанасці электрычнага поля каля паверхні Зямлі ў сярэднім складае $begin mathsize 14px style 130 straight Н over Кл end style$ . Электрычнае поле Зямлі змяняецца з цягам часу. Залішні адмоўны электрычны зарад зямнога шара вагаецца каля –6 · 10⁵ Кл.