Печатать эту главуПечатать эту главу

§ 6. Изотермический, изобарный и изохорный процессы

Примеры решения задач
Рис.
Рис. 28

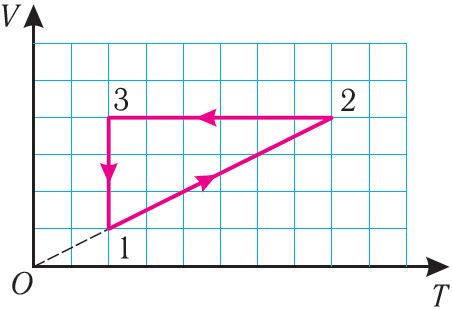
Пример 1. На рисунке 28 представлен график трёх процессов изменения состояния некоторой массы идеального газа. Как изменялись параметры газа на участках 1 rightwards arrow 2, 2 rightwards arrow 3, 3 rightwards arrow 1? Изобразите эти процессы в координатах (p, V) и (p, T).

Решение. На участке 1 rightwards arrow 2 объём газа прямо пропорционален абсолютной температуре, следовательно, процесс перехода газа из состояния 1 в состояние 2 является изобарным. Из графика следует, что в состоянии 2 температура и объём газа больше в 4 раза, чем в состоянии 1. Следовательно, в процессе изобарного расширения некоторой массы газа из состояния 1 в состояние 2 температура и объём газа увеличились. Это можно записать таким образом:

переход 1 rightwards arrow 2 colon space p space equals space const, V upwards arrow, T upwards arrow, V subscript 2 space equals space 4 V subscript 1, T subscript 2 space equals space 4 T subscript 1 space rightwards double arrow
происходит изобарное нагревание газа.

В процессе перехода газа из состояния 2 в состояние 3 остаётся постоянным объём (процесс изохорный), а температура газа уменьшается в 4 раза. Из соотношения (6.3) следует, что при изохорном охлаждении давление газа уменьшается пропорционально его абсолютной температуре. Поэтому можно записать:

переход 2 rightwards arrow 3 colon space V space equals space const, T downwards arrow, p downwards arrow, p subscript 3 space equals space T subscript 3 over T subscript 2 p subscript 2 space equals space 1 fourth p subscript 2 rightwards double arrow
происходит изохорное охлаждение газа.

Процесс перехода газа из состояния 3 в состояние 1 — изотермический. При этом объём газа уменьшается в 4 раза, что влечёт за собой, согласно закону Бойля–Мариотта, увеличение давления газа в 4 раза:

переход 3 rightwards arrow 1 colon space T space equals space const, V downwards arrow, p upwards arrow rightwards double arrow
происходит изотермическое сжатие газа.

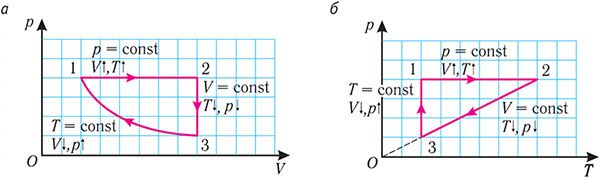
Опираясь на сделанные выводы, представим все три процесса в координатах (p, V) и (p, T) (рис. 29, а, б).

Рис.
Рис. 29

Пример 2. При изотермическом расширении идеального газа определённой массы его объём увеличился от V1 = 2,0 л до V2 = 5,0 л, а давление уменьшилось на Δp = –15 кПа. Определите первоначальное давление газа.

Дано:
V1 = 2,0 л = 2,0 · 10–3 м3
V2 = 5,0 л = 5,0 · 10–3 м3
Δp = –15 кПа = –1,5 · 104 Па
р1 — ?

Решение: Так как температура и масса газа не изменяются, то его начальное и конечное состояния связаны законом Бойля–Мариотта, т. е. p subscript 1 V subscript 1 space end subscript equals space p subscript 2 V subscript 2. С учётом того, что p subscript 2 space equals space p subscript 1 space end subscript plus space increment p, получим:

p subscript 1 V subscript 1 space equals space left parenthesis p subscript 1 plus increment p right parenthesis V subscript 2.

Откуда       fraction numerator increment p V subscript 2 over denominator V subscript 1 minus V subscript 2 end fraction.

p subscript 1 space equals space fraction numerator negative 1 comma 5 times 10 to the power of 4 space Па times 5 comma 0 times 10 to the power of negative 3 end exponent space straight м cubed over denominator 2 comma 0 times 10 to the power of negative 3 end exponent space straight м cubed minus 5 comma 0 times 10 to the power of negative 3 end exponent space straight м cubed end fraction space equals space 2 comma 5 times 10 to the power of 4 space Па space equals space 25 space кПа.

Ответ: p subscript 1 space equals space 25 space кПа.

Материал повышенного уровня

Пример 3. В двух сосудах вместимостью V1 = 20 л и V2 = 30 л находятся химически не реагирующие идеальные газы, давления которых p1 = 1,0 МПа и p2 = 0,40 МПа соответственно. Определите давление газов в сосудах после того, как их соединили тонкой короткой трубкой. Температура газов до и после соединения сосудов одинаковая.

Дано:
V1 = 20 л = 2,0 · 10-2 м3
V2 = 30 л = 3,0 · 10-2 м3
p1 = 1,0 МПа = 1,0 · 106 Па
p2 = 0,40 МПа = 4,0 · 105 Па
T = const
р — ?

Решение: Давление смеси газов равно сумме парциальных давлений (закон Дальтона): p equals p subscript 1 superscript apostrophe plus p subscript 2 superscript apostrophe. Найдём парциальное давление каждого газа после соединения сосудов. Так как температура и массы газов не изменяются, то начальное и конечное состояния каждого газа связаны законом Бойля–Мариотта, т. е.

p subscript 1 V subscript 1 equals p subscript 1 superscript apostrophe left parenthesis V subscript 1 plus V subscript 2 right parenthesis, p subscript 2 V subscript 2 equals p subscript 2 superscript apostrophe left parenthesis V subscript 1 plus V subscript 2 right parenthesis.

Следовательно, парциальные давления газов после соединения сосудов: p subscript 1 superscript apostrophe equals fraction numerator p subscript 1 V subscript 1 over denominator V subscript 1 plus V subscript 2 end fraction, p subscript 2 superscript apostrophe equals fraction numerator p subscript 2 V subscript 2 over denominator V subscript 1 plus V subscript 2 end fraction. Тогда p equals fraction numerator p subscript 1 V subscript 1 plus p subscript 2 V subscript 2 over denominator V subscript 1 plus V subscript 2 end fraction.

p equals fraction numerator 1 comma 0 times 10 to the power of 6 space Па times 2 comma 0 times 10 to the power of negative 2 end exponent space straight м cubed plus 4 comma 0 times 10 to the power of 5 space Па times 3 comma 0 times 10 to the power of negative 2 end exponent space straight м cubed over denominator 2 comma 0 times 10 to the power of negative 2 end exponent space straight м cubed plus 3 comma 0 times 10 to the power of negative 2 end exponent space straight м cubed end fraction equals 6 comma 4 times 10 to the power of 5 space Па equals 0 comma 64 space МПа.

Ответ: p = 0,64 МПа.