§ 3. Макро- и микропараметры. Идеальный газ. Основное уравнение молекулярно-кинетической теории идеального газа
Идеальный газ. Для теоретического объяснения свойств газов используют их упрощённую модель — идеальный газ.
Идеальный газ — модель газа, удовлетворяющая следующим условиям: 1) молекулы газа можно считать материальными точками, которые хаотически движутся; 2) силы взаимодействия между молекулами идеального газа практически отсутствуют (потенциальная энергия их взаимодействия равна нулю); силы действуют только во время столкновений молекул, причём это силы отталкивания.
Поведение молекул идеального газа можно описать, используя законы Ньютона и учитывая, что между соударениями молекулы движутся практически равномерно и прямолинейно.
Модель идеального газа можно использовать в ограниченном диапазоне температур и при достаточно малых давлениях. Так, например, свойства водорода и гелия при нормальном атмосферном давлении и комнатной температуре близки к свойствам идеального газа.
Изучая физику в 7-м классе, вы узнали, что давление газа на стенки сосуда, в котором он находится, как и на любое тело, помещённое внутрь сосуда, создаётся в результате ударов частиц, образующих газ (рис. 14).
![]()
Вывод основного уравнения молекулярно-кинетической теории идеального газа. С точки зрения молекулярно-кинетической теории давление газа возникает в результате ударов молекул, образующих газ, по телу, соприкасающемуся с ним (см. рис. 14). При ударе импульс молекулы газа изменяется: , где m0 — её масса, а
и
— скорости до и после удара. Если Δt — промежуток времени между двумя последовательными ударами о тело одной и той же молекулы, то средней силе
, которой тело действует на молекулу во время удара продолжительностью δt, соответствует средняя сила
, которой одна молекула действует на тело (например, на стенку сосуда) на протяжении промежутка времени Δt. Используя второй закон Ньютона для описания удара молекулы
и третий закон Ньютона для мгновенных значений сил взаимодействия молекулы и тела
, получим для введённых выше средней силы
и средней силы
с промежутком времени действия Δt:
(3.0)
При нормальных условиях и макроскопических размерах сосуда число ударов молекул газа о плоскую поверхность площадью 1 см2 составляет порядка 1024 в секунду. Очень слабые силы ударов отдельных молекул складываются для громадного количества молекул в значительную по величине и почти постоянную силу, действующую на тело. Усреднённое по времени значение этой силы, отнесённое к единичной площадке, и есть давление газа.
Пусть в сосуде, имеющем форму куба с ребром длиной l (рис. 14.1), находится идеальный газ, состоящий из одинаковых молекул массой m0 каждая. Будем считать, что молекулы упруго ударяются только о стенки сосуда, не сталкиваясь друг с другом. Так как молекулы, образующие стенки сосуда, совершают тепловые колебания, то скорости движения молекул газа при соударениях с ними изменяются случайным образом. Однако если газ и сосуд находятся в тепловом равновесии, то средняя кинетическая энергия молекул не изменяется со временем. Это позволяет реальное хаотическое движение молекул газа со всевозможными направлениями и модулями скоростей упрощённо рассматривать как движение, при котором модули проекций скорости на каждую из координатных осей одинаковые, т. е. , и остаются неизменными, а при соударениях изменяется знак только у одной из трёх проекций скорости на координатные оси.
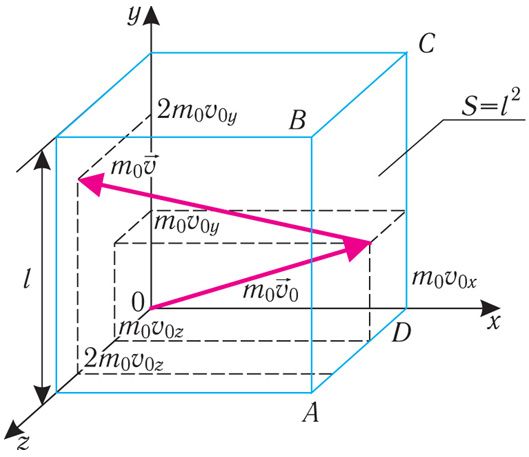
Для описания удара молекулы газа о стенку ABCD (рис. 14.1) запишем соотношение (3.1) в проекциях на координатные оси:
Так как промежуток времени между двумя последовательными соударениями молекулы со стенкой ABCD , то
Проекция полной средней силы, которой все N молекул, находящихся в сосуде, действуют на стенку ABCD, , так как
и
.
Следовательно, , где
— усреднённый по всем N частицам квадрат проекций их скоростей на ось Ох.
Разделив обе части соотношения для на площадь стенки S = l2, получим формулу для давления, оказываемого молекулами газа на стенку ABCD:
Так как , то
. Поскольку молекулы газа в среднем совершенно одинаково отражаются от трёх пар противоположно расположенных граней куба, то
. С учётом того, что объём, занимаемый газом, V = l3, а концентрация молекул газа
, получим:
(3.1)
Выражение (3.1) называют основным уравнением молекулярно-кинетической теории идеального газа. Это уравнение позволяет рассчитать макроскопический параметр давление p идеального газа через массу m0 молекулы, концентрацию n молекул и среднюю квадратичную скорость их теплового движения, определяемую по формуле . Формула (3.1) связывает между собой макро- и микроскопические параметры системы «идеальный газ».
Из основного уравнения молекулярно-кинетической теории идеального газа следует, что давление является средней величиной и, следовательно, это понятие неприменимо к отдельной молекуле.
![]()
Зависимость давления газа от среднего значения квадрата скорости теплового движения его молекул обусловлена тем, что с увеличением скорости, во-первых, возрастает импульс молекулы, а следовательно, и сила удара о стенку. Во-вторых, возрастает число ударов, так как молекулы чаще соударяются со стенками.
В герметически закрытом сосуде находится идеальный газ. Если часть газа через клапан выпустить из сосуда, то как изменятся: а) давление газа; б) плотность газа; в) количество вещества в сосуде?
Обозначим через среднюю кинетическую энергию поступательного движения молекул. Тогда основное уравнение молекулярно-кинетической теории примет вид:
.
(3.2)
Из выражения (3.2) следует, что давление идеального газа зависит от средней кинетической энергии поступательного движения его молекул и их концентрации.

На рисунке 15 представлены графики зависимости давления от концентрации для двух идеальных газов, температуры которых различны. Во сколько раз отличаются средние кинетические энергии поступательного движения молекул этих газов?

1. Назовите существенные признаки понятия «идеальный газ».
2. Каков механизм возникновения давления газа с точки зрения молекулярно-кинетической теории?
3. От чего зависит давление идеального газа?
4. В таблице указаны плотности газов при нормальных условиях:
| Газ | водород | кислород | азот | хлор |
| Плотность газа |
0,090 | 1,43 | 1,25 | 3,21 |
У молекул какого газа средняя квадратичная скорость поступательного движения максимальна?
5. В двух сосудах находятся одинаковые числа молекул идеального газа. В каком случае давления газа в сосудах будут одинаковы?
![]()
6. В баллон, содержавший определённое число атомов гелия, добавляют такое же число молекул водорода. Средняя кинетическая энергия поступательного движения молекул водорода равна средней кинетической энергии теплового движения атомов гелия. Во сколько раз изменится давление газа в баллоне?
7. В теплоизолированном герметично закрытом сосуде находится идеальный газ. Средняя кинетическая энергия молекул газа при ударах о стенки сосуда уменьшается. Нагревается ли сосуд?