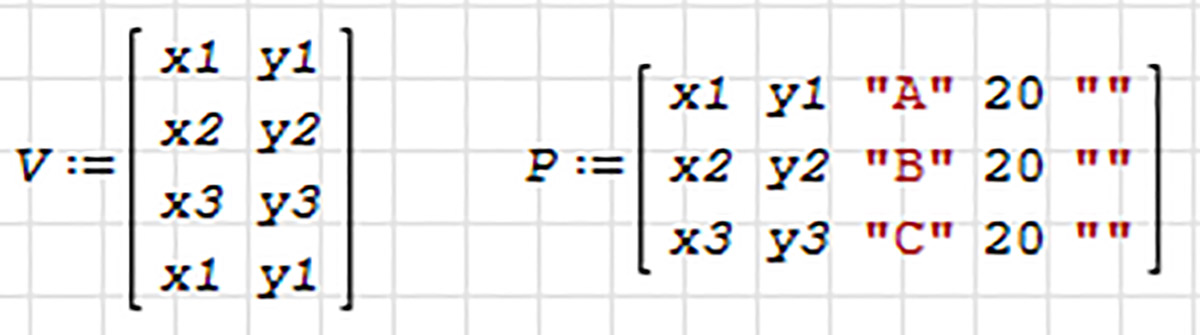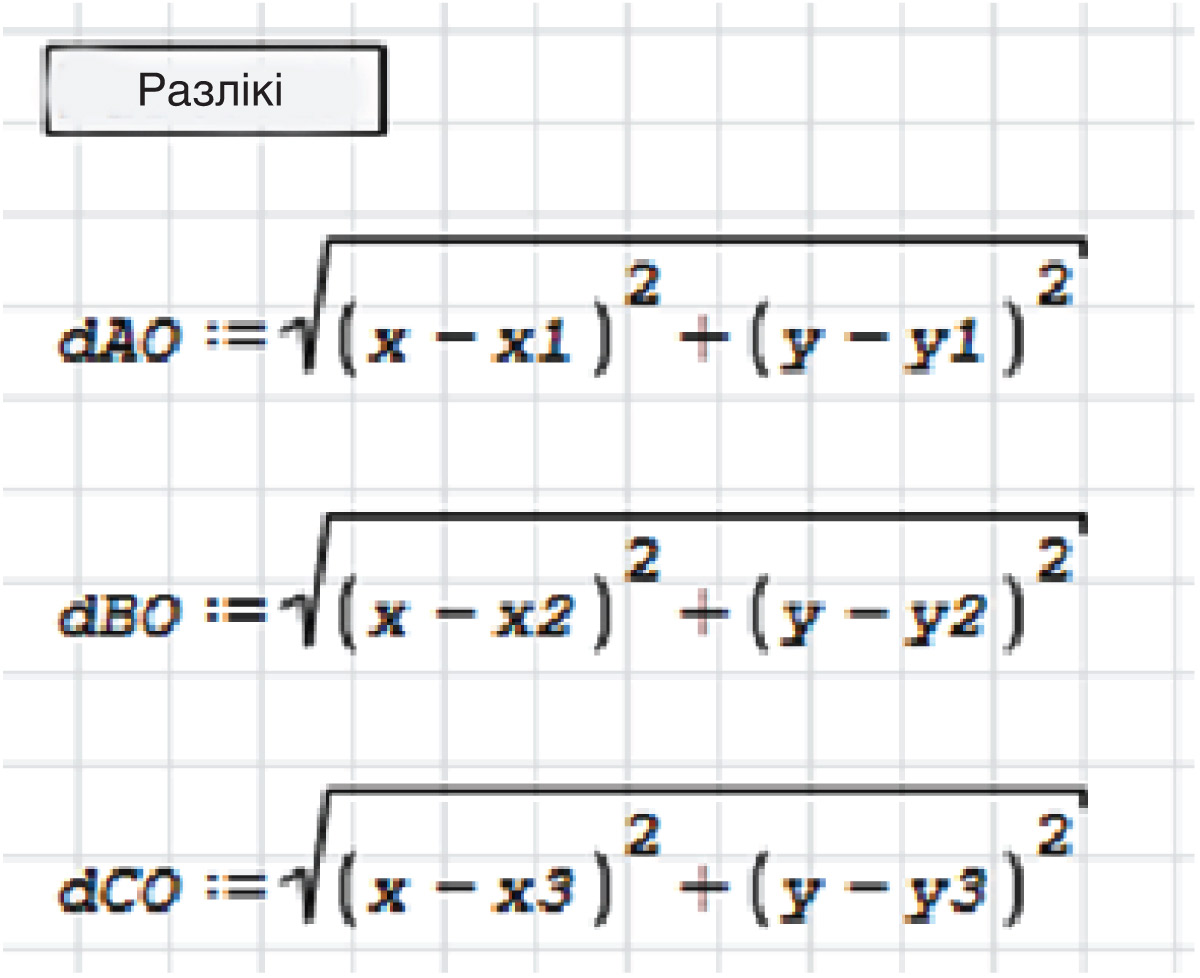§ 30. Мадэляванне ў задачах вылічэння каардынат выдатных пунктаў трохвугольніка

30.5. Стварэнне камп'ютарнай мадэлі (этап 3б)

Зыходныя даныя і пачатак разліковай табліцы размесцім па схеме, прыведзенай у прыкладзе 30.6.

На працоўным лісце заўсёды ёсць магчымасць падраўнаваць верхнія межы некалькіх абласцей або іх левыя межы (прыклад 30.7).

Тут жа ў зыходных даных ледзь ніжэй выведзем у графічнай вобласці малюнак трохвугольніка. Для гэтага падрыхтуем матрыцу каардынат вяршынь трохвугольніка і матрыцу параметраў тэксту.

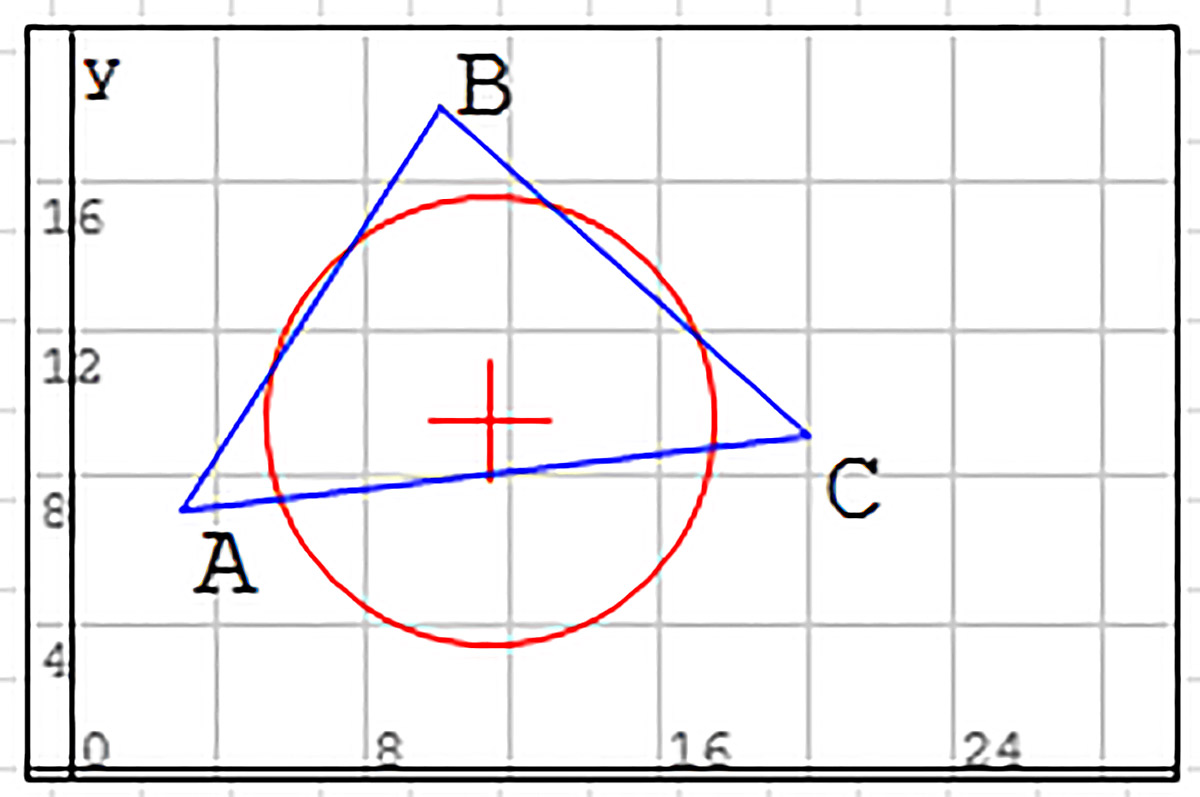
Выводзім графічную вобласць, а ў ёй выводзім вектары V і P (гл. п. 29.4). Мяняем маштаб малюнка і становішча восей так, каб у вобласці быў бачны ўвесь трохвугольнік. Каб падняць літару B у графічнай вобласці, у другім радку матрыцы P замест y2 запішам y2 +2.

Ніжэй уводзім загаловак «Разлікі» і формулы вылічэння адлегласцей ад вяршынь да цэнтра O апісанай акружнасці. Пры ўводзе падобных формул трэба максімальна выкарыстоўваць магчымасці капіравання і рэдагавання (прыклад 30.8).

Складаем вектар сістэмы S, вектар невядомых Z і вектар Zo пачатковага набліжэння (гл. п. 28.2), які выбіраецца як ацэнка каардынат цэнтра апісанай акружнасці.

Уводзім на працоўны ліст вектар пераменных і прысвойваем яму значэнне функцыі roots(), г. зн. лікавыя значэнні каардынат цэнтра акружнасці.

Вектар пераменных захоўвае рашэнне сістэмы як значэнні пераменных x і y.

Цяпер у графічнай вобласці трэба пабудаваць акружнасць і яе цэнтр (прыклад 30.9).

Прыклад 30.6. Схема размяшчэння даных і загалоўкаў мадэлі.

Прыклад 30.7. Каб выраўнаваць верхнія межы некалькіх абласцей, іх вылучаюць і пстрыкаюць па кнопцы Выровнять по горизонтали на Панели инструментов. Каб выраўнаваць левыя межы, пстрыкаюць па суседняй кнопцы Выровнять по вертикали.

Прыклад 30.8. Загаловак і формулы вылічэння адлегласцей ад вяршынь да цэнтра O.

Першую формулу можна вылучыць, скапіраваць у буфер абмену і копію ўставіць ніжэй першай формулы. У другой формуле застаецца выправіць адну літару і два нумары каардынат. Аналагічна капіраваннем уводзіцца і трэцяя формула.

Прыклад 30.9. Атрыманыя значэнні каардынат захаваны як значэнні пераменных x і y, і выкарыстоўваць іх у графічнай вобласці, якая размешчана на працоўным лісце вышэй, немагчыма. Таму пабудуем новую графічную вобласць ніжэй.

Для гэтага вылучаем вектар P і графічную вобласць з трохвугольнікам з зыходных даных, капіруем іх у буфер абмену і ўстаўляем копіі на ліст ніжэй матэматычнай вобласці, у якой атрымана рашэнне сістэмы ўраўненняў.

Пстрыкаем па правым ніжнім вуглу матрыцы-копіі параметраў тэксту P, націскаем клавішу Пробел (з'яўляецца вуглавая метка) і дапаўняем матрыцу P двума радкамі.