§ 28. Фатон. Ураўненне Эйнштэйна для фотаэфекту

Вывучэнне законаў фотаэфекту прывяло вучоных да нечаканай высновы: пры ўзаемадзеянні з рэчывам (паглынанні ці выпраменьванні) святло паводзіць сябе падобна часціцам, якія рухаюцца (квантам). Што гэта за часціцы? Якія іх уласцівасці і як яны звязаны з хвалевымі характарыстыкамі святла?

Развіваючы ідэі М. Планка, А. Эйнштэйн у 1905 г. для тлумачэння эксперыментальных законаў знешняга фотаэфекту прапанаваў гіпотэзу аб дыскрэтнасці самога электрамагнітнага выпраменьвання — святло выпраменьваецца, паглынаецца і распаўсюджваецца ў выглядзе асобных порцый (квантаў). Ён разгледзеў элементарныя працэсы паглынання і выпускання гэтых квантаў.
Паводле гіпотэзы Эйнштэйна монахраматычнае электрамагнітнае выпраменьванне частатой  мае не толькі хвалевыя ўласцівасці, але і ўласцівасці, характэрныя для патоку часціц. Кожная такая часціца рухаецца са скорасцю святла с і нясе квант энергіі . Назваць гэтыя часціцы фатонамі прапанаваў у 1928 г. амерыканскі фізік Артур Комптан.
Энергія фатона можа быць выражана праз даўжыню хвалі λ:

(1)

З рэлятывісцкага азначэння імпульсу  для фатона  вынікае, што модуль яго імпульсу вызначаецца выразамі:

(1-1)

Значыць, для фатона:

Выключыўшы скорасць  з рэлятывісцкіх выразаў імпульсу і эненргіі цела:

,  ,

атрымаем суадносіну

.

(1-2)

Для фатона  з формулы (1-2) знаходзім, што маса фатона роўна нулю (m = 0).

Маса фатона, які рухаецца са скорасцю святла ў вакууме, роўна нулю.
Такім чынам, фатон — дзіўная часціца, якая мае энергію E = hν, імпульсам . З прычыны таго што скорасць фатона роўна скорасці святла ў вакууме, яго маса роўна нулю (m = 0). Такія часціцы называюць бязмасавымі.
Фатон з’яўляецца элементарнай часціцай, толькі ў адрозненне ад іншых элементарных часціц ён не мае масы, а таму «вымушаны» заўсёды рухацца са скорасцю распаўсюджвання святла.
Такім чынам, фатон мае наступныя ўласцівасці:

- існуе толькі ў руху;
- з’яўляецца бязмасавай часціцай (m = 0);
- электрычна нейтральны (q = 0);
- скорасць яго руху роўна скорасці распаўсюджвання святла ў вакууме ва ўсіх  ІСА;
- энергія фатона прапарцыянальна частаце адпаведнага электра­маг­нітнага выпраменьвання (E = hν)
- модуль імпульсу фатона роўны адносіне яго энергіі да модуля скорасці руху ().

Разгледзім тлумачэнне эксперыментальных законаў фотаэфекту, прапанаванае Эйнштэйнам на падставе квантавых уяўленняў. Пры асвятленні электрода электрамагнітным выпраменьваннем (гл. мал. 171) адбываецца ўзаемадзеянне фатонаў з электронамі рэчыва. Калі энергія фатона E = hν досыць вялікая, то які-небудзь з электронаў пасля паглынання фатона можа атрымаць энергію, дастатковую для таго, каб пакінуць апраменьваемы ўзор. Электроны, якія пакінулі ўзор, маюць некаторую скорасць, таму нават пры адсутнасці напружання паміж электродамі сіла фотатоку не роўна нулю. Менавіта таму вольт-амперная характарыстыка фотаэфекту пры напружанні, роўным нулю, не праходзіць праз нуль (гл. мал. 172, в).
Для таго каб пакінуць рэчыва, электрон павінен выканаць работу супраць сіл узаемадзеяння электрона з атамамі рэчыва. Такім чынам, мінімальная энергія, неабходная для выбывання электрона з паверхні рэчыва, называецца работай выхаду і абазначаецца А_вых(А_вых > 0). Для металаў гэта работа звязана з пераадоленнем сіл узаемадзеяння электронаў з дадатна зараджанымі іонамі крышталічнай рашоткі, якія ўтрымліваюць электрон у рэчыве. Работа выхаду для металаў звычайна складае некалькі электрон-вольт (табл. 9).

Табліца 9. Фотаэлектрычныя характарыстыкі некаторых рэчываў

Рэчыва			λк, нм
Цэзій	1,9	4,6	650
Калій	2,2	5,3	560
Натрый	2,3	5,6	540
Кальцый	2,7	6,5	460
Цынк	3,7	8,9	340
Серабро	4,3	10	260
Вальфрам	4,5	11	280
Нікель	5,0	12	250
Плаціна	5,3	13	230

Астатняя частка энергіі паглынутага кванта складае кінэтычную энер­гію электрона, які вызваліўся. Найбольшую кінетычную энергію   будуць мець тыя электроны, якія паглынуць кванты святла паблізу ад паверхні металу і выляцяць з яго, не паспеўшы згубіць энергію пры сутыкненнях з іншымі часціцамі ў метале.
На падставе закону захавання энергіі можна запісаць наступнае ўраўненне для фотаэлектрона:

.

(2)

Гэту суадносіну называюць ураўненнем Эйнштэйна для знешняга фотаэфекту.
Адзначым, што — гэта максімальная кінетычная энергія электрона , якую ён можа мець, вылецеўшы з рэчыва.
З-за розных страт кінетычная энергія электрона будзе меншай за раз­ліковае значэнне.

Выкарыстаўшы ўраўненне Эйнштэйна, можна растлумачыць эксперыментальныя законы фотаэфекту.

Тлумачэнне першага закону фотаэфекту. Сіла фотатоку насычэння прапарцыянальна агульнаму ліку фотаэлектронаў, якія пакідаюць паверхню металу за адзінку часу. Лік такіх фотаэлектронаў, у сваю чаргу, прапарцыянальны ліку фатонаў, якія падаюць на паверхню за гэты ж час. Менавіта прапарцыянальна, а не роўна, паколькі частка квантаў святла паглынаецца крышталічнай рашоткай, і іх энергія пераходзіць ва ўнутраную энергію металу. Такім чынам, павелічэнне інтэнсіўнасці падаючага святла прыводзіць да росту ліку фотаэлектронаў, якія пакідаюць паверхню металу.

Тлумачэнне другога закону фотаэфекту. Фотаэлектрон вырываецца з катода за кошт дзеяння аднаго кванта падаючага выпраменьвання. Таму кінетычная энергія фотаэлектрона залежыць не ад поўнай энергіі хвалі, а ад энергіі аднаго кванта, г. зн. частаты . Пры павелічэнні частаты n падаючага святла максімальная кінетычная энергія  фотаэлектронаў нарастае лінейна, як вынікае з ураўнення Эйнштэйна для фотаэфекту (2), згодна з суадносінай:

(3)

Вядома, што фотатокам можна кі­ра­ваць, падаючы на металічныя плас­ціны розныя напружанні. Калі на сістэму падаць невялікае напружанне адваротнай палярнасці, якое «абцяжарвае» вылет электронаў, то сіла току паменшыцца, паколькі цяпер фотаэлектронам, акрамя работы выхаду, прыйдзецца выконваць дадатковую работу супраць сіл электрычнага поля.
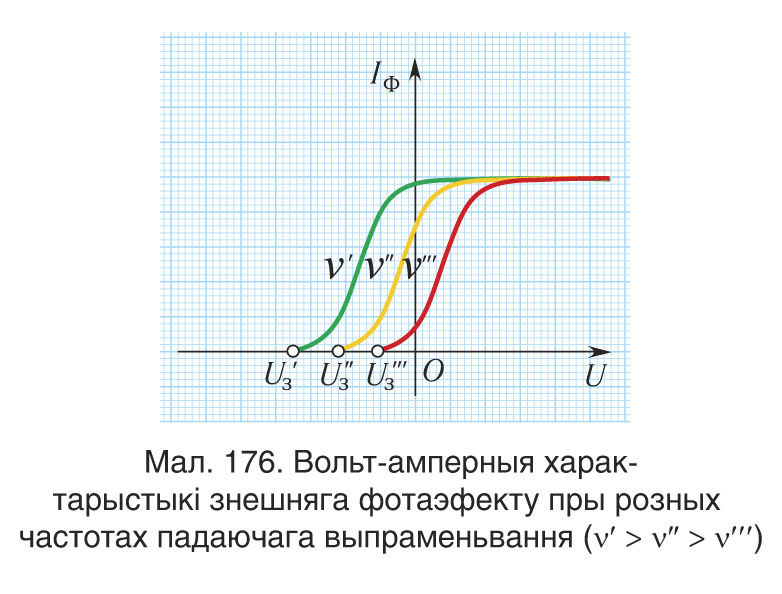
Пры некаторым адмоўным значэнні напружання U_з электроны затарможваюцца і, не дасягнуўшы паверхні анода, вяртаюцца на катод. Сіла току ў ланцугу пры гэтым будзе роўна нулю (мал. 176). Велічыню U_з, пры якой сіла току ў ланцугу роўна нулю, называюць затрымліваючым напружаннем. Такім чынам, уся кінетычная энергія электронаў затрачваецца на работу супраць сіл электрычнага поля. Пры гэтым максімальная кінетычная энергія электронаў выражаецца праз затрымліваючае напружанне наступным чынам :

(4)

Тлумачэнне трэцяга закону фотаэфекту. Калі частата v падаючага выпраменьвання меншая за гранічную частату  пры якой , то выпусканне электронаў не адбываецца . Такім чынам, фотаэфект адсутнічае, калі частата выпраменьвання аказваецца меншай за некаторую характэрную для дадзенага рэчыва велічыню
Значыць, чырвоную мяжу фотаэфекту можна знайсці з умовы:

(5)

Яна залежыць толькі ад работы выхаду электронаў, г. зн. вызначаецца будовай металу і станам яго паверхні.
Даўжыня хвалі  выпраменьвання, якая адпавядае чырвонай мяжы фотаэфекту, можа быць вызначана з суадносіны:

(6)

З ураўнення Эйнштэйна для фотаэфекту (2) вынікае, што, знайшоўшы тангенс tg α вугла нахілу прамых ліній на малюнку 174, можна вылічыць пастаянную Планка, паколькі

а па пунктах перасячэння прадаўжэння графікаў (гл. мал. 175) з восямі U_з і  — знайсці работу выхаду А_вых і чырвоную мяжу для дадзенага рэчыва.

У наш час цяжка ўявіць сабе сучасную навуку і тэхніку без выкарыстання прылад (прыёмнікаў выпраменьвання), якія пераўтвараюць светлавыя сігналы ў электрычныя. Такія прылады называюцца фотаэлементамі (мал. 177).

Фотаэлементы выкарыстоў­ваюцца для кантролю пасажырапатоку ў метро, для ўключэння і выключэння асвятлення на вуліцах, для кіравання вытворчымі працэсамі, у ваеннай тэх­ніцы: у саманаводных снарадах, для сігналізацыі і лакацыі. Інфра­чырвоныя фотаэлементы шырока выкарыстоўваюцца ў пультах дыстанцыйнага кіравання рознымі бытавымі электроннымі прыборамі (тэлевізар, кандыцыянер і г. д.).

У 1921 г. пры прысуджэнні Альберту Эйнштэйну Нобелеўскай прэміі па фізіцы ў рашэнні Нобелеўскага камітэта падкрэслівалася, што «прэміяй асабліва адзначаецца тлумачэнне законаў фотаэлектрычнага эфекту». Першы фотаэлемент на знешнім фотаэфекце быў створаны Сталетавым у 1888 г.