§ 1. Вагальны рух. Гарманічныя ваганні

У свеце разнастайных механічных рухаў даволі часта сустракаюцца перыядычныя рухі (рухі, якія паўтараюцца): ваганні маятніка гадзінніка, рух поршня ў рухавіку аўтамабіля, біццё сэрца чалавека. У чым асаблівасці такіх рухаў? Якімі параметрамі яны апісваюцца? У чым іх адрозненні ад паступальнага і вярчальнага руху?

Розныя віды механічнага руху характарызуюцца рознай ступенню паўтаральнасці. Так пры паступальным руху цела можа наогул не вярнуцца ў зыходнае становішча, у той час як пры вярчальным руху гэта адбудзецца праз прамежак часу, роўны перыяду абарачэння T.
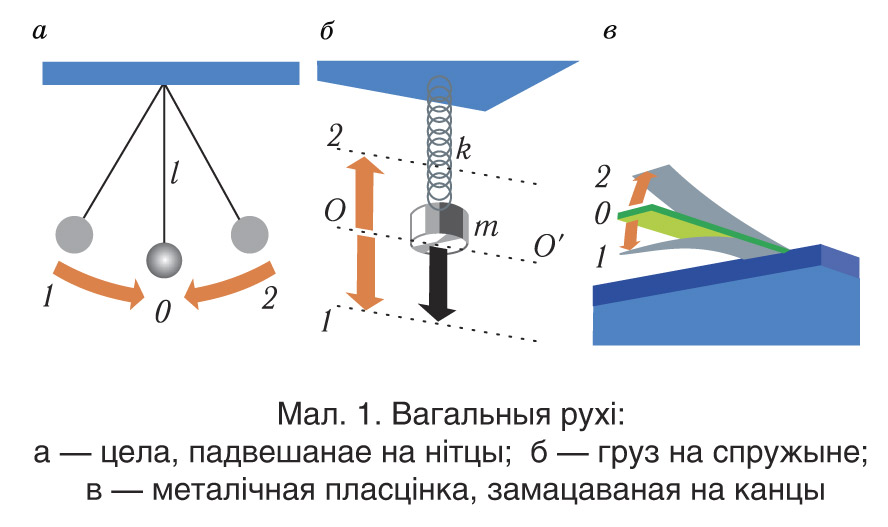
У навакольным свеце вельмі шырока распаўсюджаны і такі від руху цела, пры якім яно спачатку рухаецца ў адным напрамку, а затым — у зваротным, і такі рух паўтараецца неаднаразова па адной і той жа траекторыі. Падобныя прыклады прыведзены на малюнку 1. Пры гэтым праз любы пункт траекторыі, за выключэннем крайніх пунктаў 1 і 2 (гл. мал. 1), цела праходзіць як у прамым, так і ў зваротным напрамках.

Такі від руху называецца вагальным. Вагальны рух здзяйсняюць такія механічныя сістэмы, як маятнік, арэлі, лісце дрэў пад уздзеяннем ветру, струны пры гульні на гітары ці піяніна. Рух атамаў у крышталічнай рашотцы таксама мае вагальны характар.
Такім чынам, для вагальнага руху ха­рак­тэрна ўласцівасць вяртальнасці (гл. мал. 1).
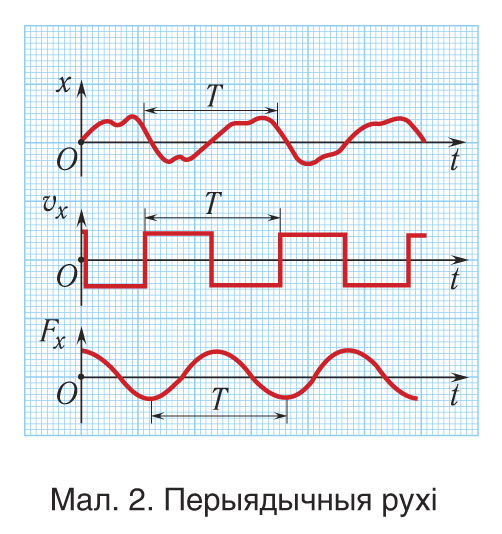
Калі фізічныя велічыні, якія характарызуюць рух (напрыклад, каардыната x праекцыі скорасці  і дзеючай сілы ), прымаюць адны і тыя ж значэнні праз роўныя прамежкі часу (мал. 2), то такія ваганні (рухі) называюцца перыядычнымі. Мінімальны прамежак часу, па закан­чэнні якога паўтараюцца значэнні ўсіх фізічных велічынь, што характарызуюць ваганне, называецца перыядам ваганняў і абазначаецца літарай T:

                 (1)

дзе Δt  — прамежак часу, за які адбылося N ваганняў.

Ваганні па сваёй прыродзе могуць быць не толькі механічнымі, але і электрамагнітнымі (перыядычныя змяненні напружання і сілы току ў электрычным ланцугу), тэрмадынамічнымі (ваганні тэмпературы з цягам часу) і г. д. Такім чынам, ваганні — гэта асобая форма руху ў тым сэнсе, што розныя па сваёй прыродзе фізічныя працэсы (механічныя, электрамагнітныя і г. д.) апісваюцца аднолькавымі матэматычнымі залежнасцямі фізічных велічынь ад часу.
Для апісання ваганняў, як і для вярчальнага руху, разам з перыядам ваганняў T выкарыстоўваюць велічыню, якая называецца частатой ваганняў. Яна абазначаецца літарай ν. Частата ν роўна адносіне ліку ваганняў N да прамежку часу Δt, за які яны адбыліся:

                                           (2)

Такім чынам, частата ваганняў паказвае, які лік ваганняў цела выконвае за адзінку часу (за секунду):

(3)

Акрамя частаты , часта выкарыстоўваюць цыклічную частату , якая паказвае лік ваганняў, выконваемых за прамежак часу Δt, роўны 2π секунд:

(4)

Для нагляднага апісання вагальнага руху зручна прадставіць залежнасць каардынаты x цела, якое вагаецца, ад часу t у выглядзе графіка, г. зн. пабудаваць графік функцыі x(t).
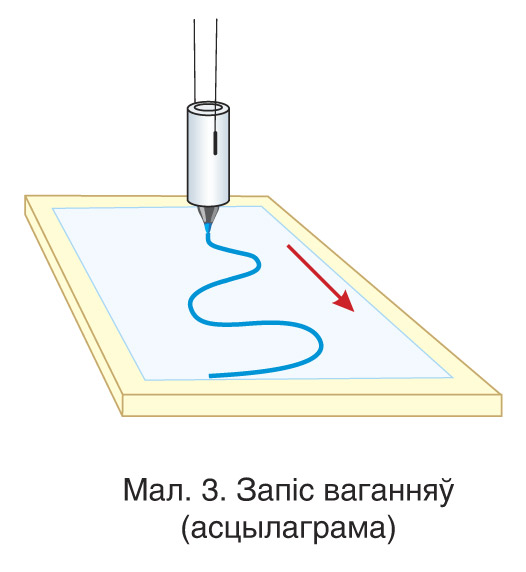
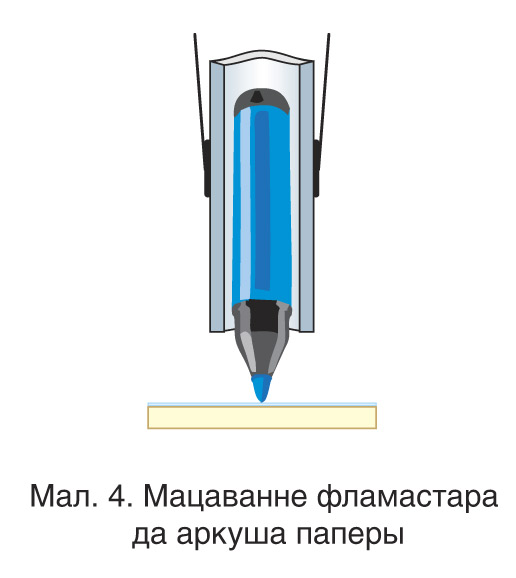
Для механічнага «запісу» ваганняў можна выкарыстоўваць устаноўку, паказаную на малюнку 3. У гэтай устаноўцы да грузу, падвешанага на дзвюх нітках, прымацаваны фламастар (мал. 4). Ён можа вольна перасоўвацца ў трубачцы для таго, каб увесь час дакранацца да аркуша паперы пры ваганнях грузу. Калі адхіліць груз папярок аркуша паперы і адпусціць, то кончык фламастара будзе апісваць на аркушы прамую лінію, якая з’яўляецца траекторыяй руху грузу (мал. 5).

             

Калі ж пры гэтым аркуш паперы будзе рухацца з пастаяннай скорасцю, то адбудзецца складанне двух рухаў ва ўзаемна перпендыкулярных напрамках. У выніку на паперы з’явіцца крывая (гл. мал. 3), кожны пункт якой адпавядае становішчу фламастара, які вагаецца, у розныя моманты часу. Атрымалася разгортка вагальнага руху, г. зн. графік руху цела, якое вагаецца.
Такая крывая называецца асцылаграмай (ад лац. oscillum — ваганне і грэч. γραμα (грама) — запіс).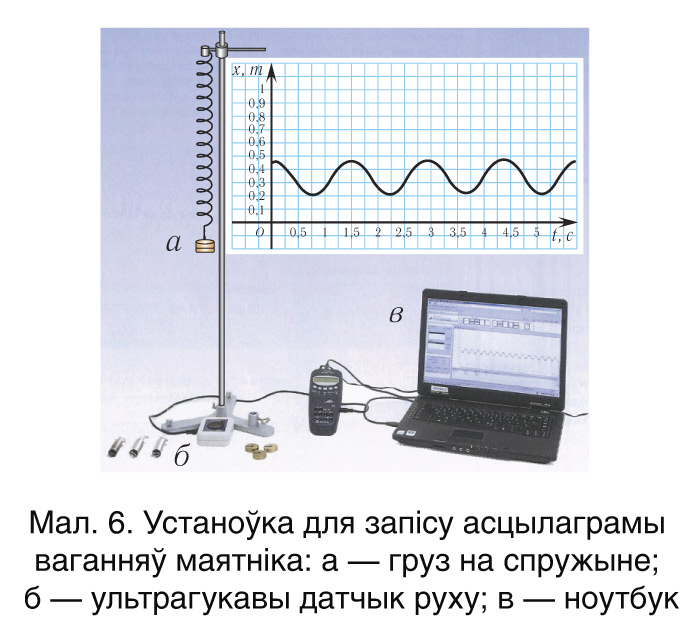
Для разгорткі ваганняў можна вы­карыстоўваць і сучасную ўстаноўку з камп’ютарам, паказаную на малюн­ку 6. Падвесім на цыліндрычнай спружыне груз. Адвядзём яго ўніз, адпусцім і будзем рэгістраваць ваганні з дапамогай ультрагукавога датчыка руху. Ён бу­дзе вызначаць адлегласць да падвешанага грузу. Пры адпаведным праграмным забеспячэнні залежнасць адлегласці па­між грузам і датчыкам ад часу бу­дзе паказвацца на экране камп’ютара (гл. мал. 6).
Якія высновы можна зрабіць зыхо­дзячы з прадстаўленых асцылаграм?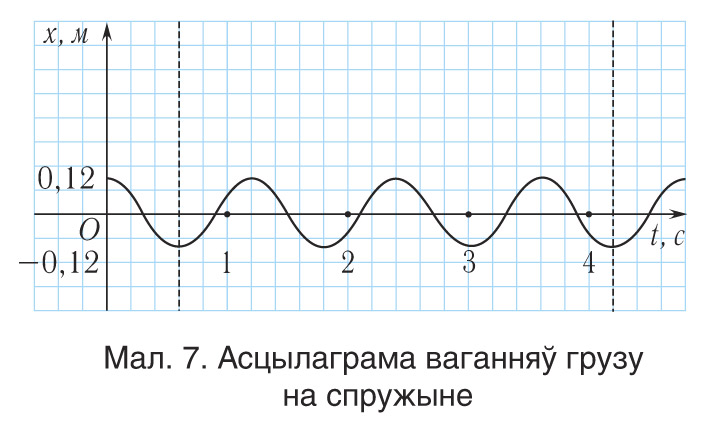
Па-першае, каардыната цела змяняецца перыядычна (гл. мал. 6). Звычайна сістэму каардынат выбіраюць так, што вось часу праходзіць праз пункт, значэнне каардынаты
х = 0 якога адпавядае стано­вішчу ўстойлівай раўнавагі (мал. 7). У такім разе каардыната грузу будзе змяняцца
ад максімальнага значэння x = x_max= A да мінімальнага значэння x = x_min = −A. Максімальнае адхіленне маятніка ад значэння х = 0 (становішча раўнавагі) называецца амплітудай ваганняў і абазначаецца літарай А. У дадзеным выпадку яе велічыня роўна А = 0,12 м.
Такім чынам, ваганні, акрамя перыяду (частаты), характарызуюцца амплітудай ваганняў.
Па-другое, скорасць і паскарэнне пры руху цела, якое вагаецца, непастаянныя ў часе. Яны таксама перыядычна змяняюцца з цягам часу. Так, скорасць маятніка максімальная (v = v_max) пры праходжанні становішча раўнавагі (х = 0) і роўна нулю (v = 0) пры х = A або х = −A.
Форму крывой, якая выражае залежнасць змянення велічыні, што вагаецца (напрыклад, каардынаты, праекцыі скорасці, праекцыі паскарэння), ад часу, называюць формай ваганняў (гл. мал. 2).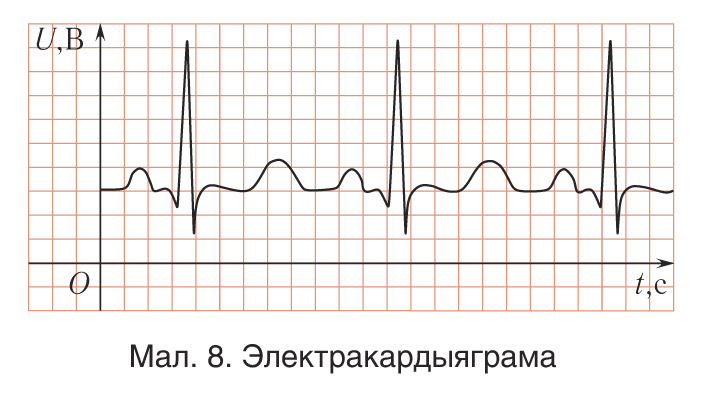
Асцылаграмы розных ваганняў шырока выкарыстоўваюцца ў медыцыне, навуцы і тэхніцы. Ваганні, якія выконваюць грузы, падвешаныя на спружыне або нітцы, з’яўляюцца найбольш простымі па форме (сінусаідальнымі або косінусаідальнымі) (гл. мал. 7). На малюнку 8 паказана электракардыяграма (ад грэч. καρδια (кардыё) — сэрца) — запіс біцця сэрца чалавека, які дазваляе вызначыць стан сэрца і, калі неабходна, прызначыць своечасовае лячэнне.
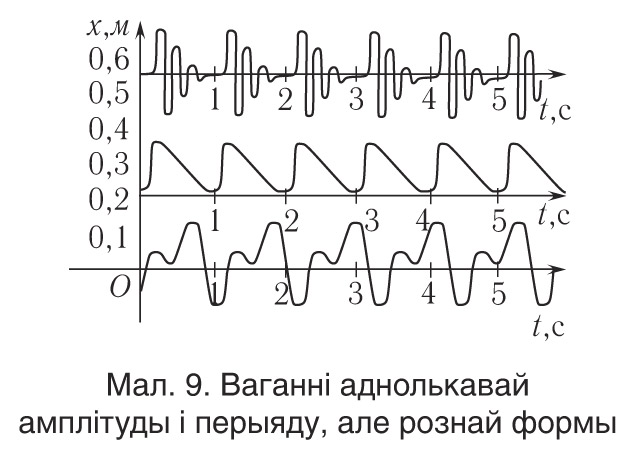У адрозненне ад асцылаграмы грузу, які вагаецца (гл. мал. 7), форма электракардыяграмы (гл. мал. 8) значна больш складаная.
Заўважым, што амплітуда і перыяд ваганняў не даюць поўнага ўяўлення аб характары перыядычнага працэсу, бо працэсы могуць мець аднолькавую амплітуду і перыяд, але зусім розную форму (мал. 9).
Як жа матэматычна апісваюцца гарманічныя ваганні?
Яны апісваюцца ўраўненнямі, у якіх каардыната (зрух) цела змяняецца з цягам часу па законе косінуса.

(5)

                 

або сiнуса

(6)

Велiчыня  называецца фазай ваганняў. Яна вызначае стан вагальнай сістэмы (каардынаты, скорасці, паскарэння) у любы момант часу пры зададзенай частаце і амплітудзе. Значэнне ў пачатковы момант часу φ(t = 0) =φ₀ называецца пачатковай фазай  φ₀.

Залежнасць каардынаты ад часу x(t) (суадносіны (5) і (6)) называецца кінематычным законам руху, паколькі дазваляе вызначыць становішча цела, якое вагаецца. Зыходзячы з яго можна знайсці яго скорасць, паскарэнне ў любы момант часу.
Каардыната цела (зрух цела са становішча раўнавагі) x(t) у момант часу t пры перыядычным руху падпарадкоўваецца роўнасці:

дзе f(t) — зададзеная перыядычная функцыя ад часу t, T — перыяд гэтай функцыі.
Рух, пры якім каардыната цела змяняецца з цягам часу па законе сінуса (або косінуса), называецца гарманічным ваганнем.
Такім чынам, асноўнымі кінематычнымі велічынямі, якія характарызуюць перыядычныя ваганні, з’яўляюцца: перыяд (Т), частата (), цыклічная частата () і амплітуда (А).
У СІ асноўнымі адзінкамі гэтых велічынь з’яўляюцца: перыяду ваганняў — секунда (1 c), частаты ваганняў — герц (1 Гц), цыклічнай частаты — 1 c⁻¹. 1 Гц роўны частаце ваганняў цела, пры якой за 1 c цела выконвае адно поўнае ваганне (1 Гц = 1 с⁻¹).

Назва адзінкі частаты герц дадзена ў гонар нямецкага фізіка Генрыха Герца, які эксперыментальна адкрыў электрамагнітныя хвалі.

Звернем увагу на тое, што велічыні T, , , A, якія характарызуюць гарманічныя ваганні цела, аналагічныя адпаведным велічыням, якія апісваюць рух цела па акружнасці (табл. 1).

 Т а б л и ц а  1. Сопоставление физических величин, характеризующих вращательное и колебательное движение 

Фізічныя велічын	Від руху
	Рух па акружнасці	Гарманічныя ваганні
R, A	R — радыус акружнасці	А — амплітуда ваганняў
φ	Вугал павароту	Фаза ваганняў
T	Перыяд абарачэння	Перыяд ваганняў
N	Лік абаротаў	Лік ваганняў
	Частата абарачэння	Частата ваганняў
	Вуглавая скорасць	Цыклічная частата

Частата  (перыяд T) гарманічных ваганняў залежыць толькі ад уласцівасцей сістэмы, у якой адбываюцца ваганні. Амплітуда ваганняў A і пачатковая фаза  вызначаюцца не ўласцівасцямі самой сістэмы, а тым спосабам, якім у сістэме выкліканы ваганні. Так, ваганні можна ўзбудзіць адхіленнем ад становішча раўнавагі, а можна — штуршком са становішча раўнавагі.
Усе велічыні, разгледжаныя вышэй, а іменна перыяд T (1), частата  (3), цыклічная частата  (4) і амплітуда A, вызначаюць вагальны працэс у цэлым, незалежна ад яго прыроды.