§ 21. Формула тонкой линзы

Одним из простейших оптических приборов является тонкая линза (рис. 144), которая широко используется как для исправления дефектов зрения, так и для получения оптических изображений. Какие изображения дает тонкая линза? Как связаны между собой расстояние от предмета до тонкой линзы и расстояние от линзы до изображения?

Линза называется собирающей, если после преломления в ней параллельный пучок становится сходящимся (рис. 145, а). Если же после преломления в линзе параллельный пучок становится расходящимся, то линза называется рассеивающей (рис. 145, б).

Величина, обратная фокусному расстоянию линзы, выраженному в метрах, называется ее оптической силой: .

Единица оптической силы — диоптрия (1 дптр). 1 дптр соответствует оптической силе линзы с фокусным расстоянием $F space equals space 1 straight м$ ; 1дптр = 1м^-1

Линзы можно представить в виде совокупности трехгранных призм. На рисунке 145 изображена модель двояковыпуклой линзы, собранной из призм, повернутых основаниями к центру линзы (см. рис. 145, а). Соответственно, модель двояковогнутой линзы будет представлена призмами, повернутыми основаниями от центра линзы (см. рис. 145, б). Преломляющие углы этих призм можно подобрать таким образом, чтобы падающие на нее параллельные лучи после преломления в призмах собрались в одной точке F (см. рис. 145, 146).

Линза считается тонкой, если ее толщина в центре намного меньше радиусов ограничивающих ее поверхностей. Тонкая линза дает неискаженное изображение только в том случае, если свет монохроматический и предмет достаточно мал, следовательно, лучи распространяются вблизи главной оптической оси.
Отметим условия, при одновременном выполнении которых линза является собирающей (рис. 147, а):
— толщина в центре больше толщины у краев;
— ее показатель преломления больше показателя преломления окружающей среды.

При невыполнении (или выполнении) только одного из этих условий линза является рассеивающей (рис. 147, б):
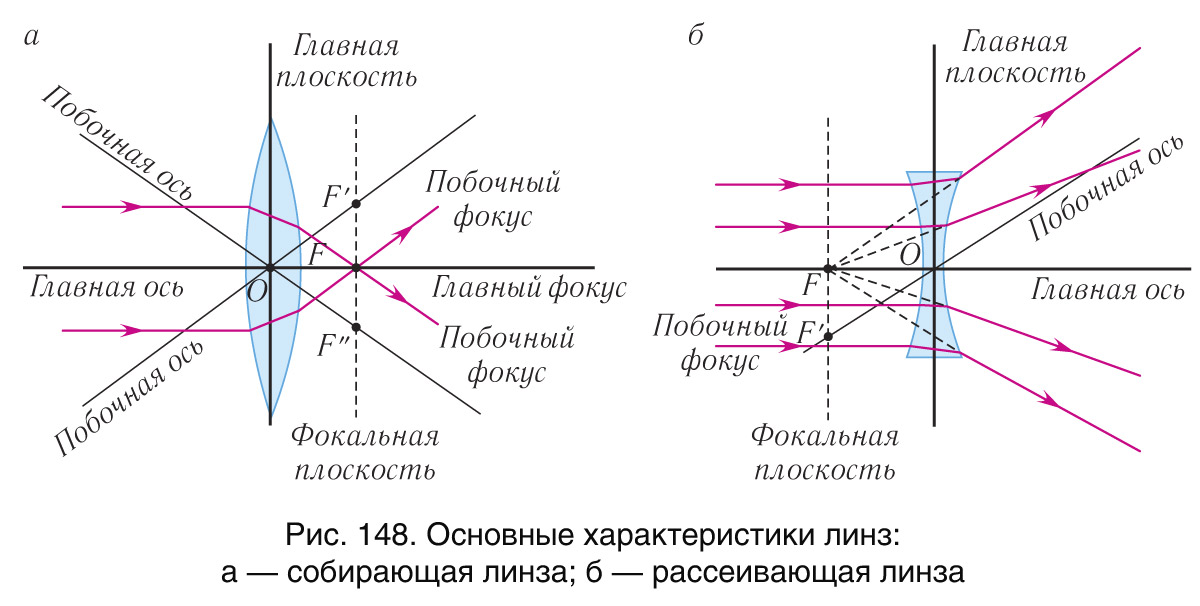
Рассмотрим основные характеристики линзы (рис. 148 а, б).

Прямая линия, на которой лежат центры обеих сферических поверхностей линзы, называется главной оптической осью.
Точка линзы, проходя через которую луч не преломляется, называется оптическим центром.
Прямая линия, проходящая через оптический центр линзы, не совпадающая с главной оптической осью, называется побочной оптической осью. Каждая линза имеет только одну главную оптическую ось и бесконечно много побочных осей.
Плоскость, проходящая через оптический центр тонкой линзы перпендикулярно главной оптической оси, называют главной плоскостью линзы.
Точка, в которую собирается узкий пучок света после преломления в линзе, распространяющийся параллельно главной оптической оси, называется главным фокусом F линзы. Расстояние OF от оптического центра линзы до ее главного фокуса, называется фокусным расстоянием линзы.

Плоскость, проходящая через главный фокус перпендикулярно главной оптической оси, называется фокальной плоскостью. Фокальная плоскость собирающей линзы является геометрическим местом точек, в которых пересекаются параллельные лучи, падающие на линзу под любым углом к главной оптической оси. Поэтому, пучок света, направленный на собирающую линзу параллельно побочной оптической оси, собирается в побочном фокусе.

Построение изображений

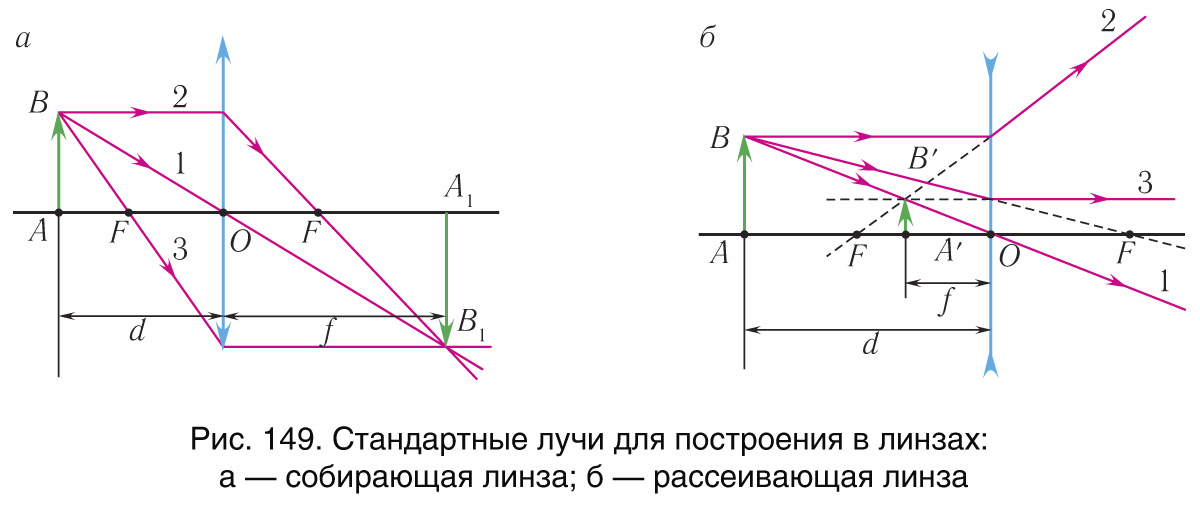
Обычно для построений в линзах используют три характерных (стандартных) луча (рис. 149 а, б):

- луч (1), идущий через оптический центр линзы, не испытывает преломления;
- луч (2), параллельный главной оптической оси, после преломления проходит через главный фокус;
- луч (3), проходящий через главный фокус, после преломления идет параллельно главной оптической оси.

Для построения изображения в линзе достаточно построить ход двух лучей от каждой точки предмета (см. рис. 149). Изображение находится в месте пересечения лучей после преломления на поверхностях линзы (действительное изображение) или в месте пересечения продолжений лучей (мнимое изображение).

Отметим, что если предмет AB расположен перпендикулярно главной оптической оси, то и его изображение $A subscript 1 B subscript 1$ будет перпендикулярно этой оси. Поэтому достаточно построить только изображение $A subscript 1$ точки предмета A, а изображение $B subscript 1$ точки B находим, опуская перпендикуляр из точки $B subscript 1$ на главную оптическую ось (см. рис. 149).
Для построения изображения точки, находящейся на главной оптической оси, кроме луча, проходящего через центр линзы, используют луч, падающий на нее параллельно какой либо побочной оптической оси (рис. 150). Этот луч после преломления в линзе пройдет через побочный фокус , лежащий на побочной оси. Такие построения приведены для собирающей и рассеивающей линз на рис. 150. На рисунке 151 приведен пример построения области видения предмета S в тонкой линзе.

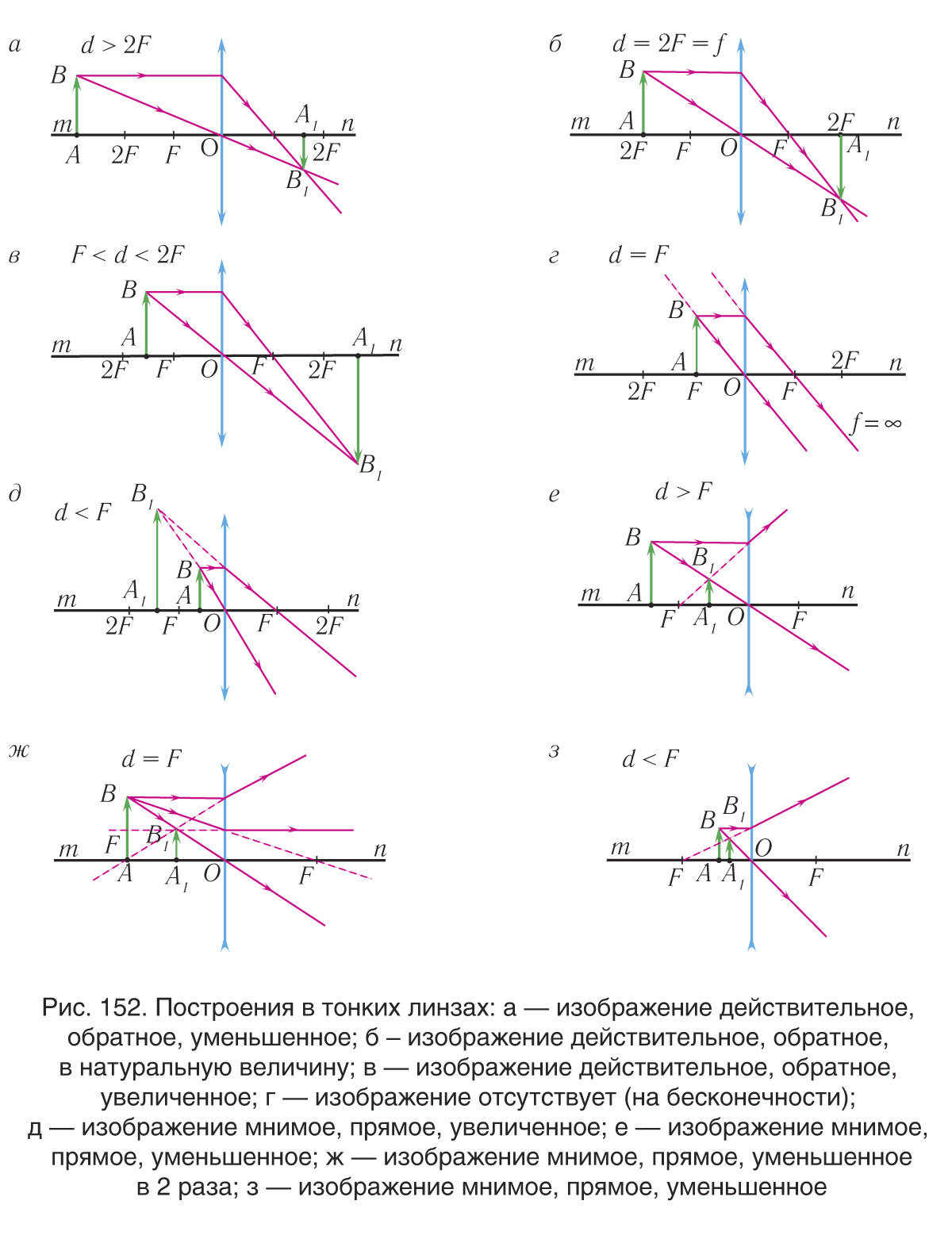
Характеристики изображений

В зависимости от типа линзы и расстояния до нее можно получать изображения: увеличенные и уменьшенные, прямые и обратные (перевернутые), действительные и мнимые (рис. 152).

Между фокусным расстоянием тонкой линзы, расстоянием от предмета до линзы и от линзы до изображения существует определенная количественная зависимость, называемая формулой тонкой линзы.
Выведем формулу тонкой линзы из геометрических соображений, рассматривая ход характерных лучей. Луч, идущий через оптический центр O линзы, луч, параллельный главной оптической оси линзы, и луч, проходящий через главный фокус линзы.
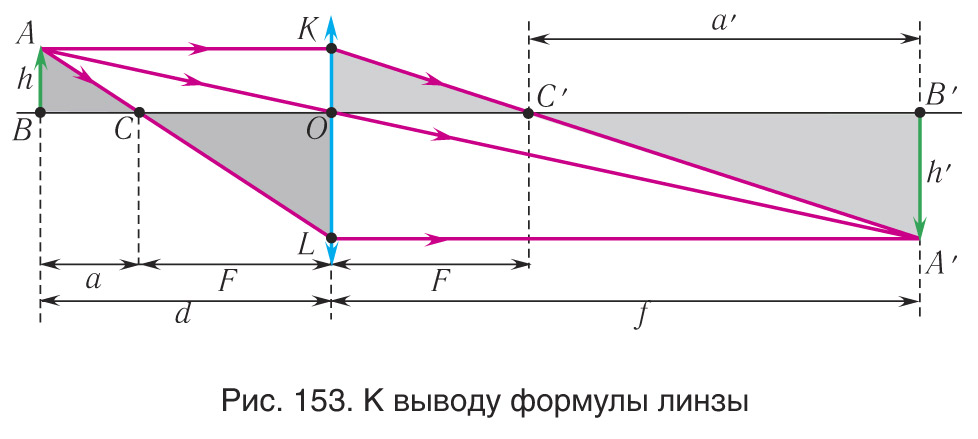
Построим изображение предмета AB в тонкой собирающей линзе (рис. 153). Пусть расстояние от предмета до линзы d, расстояние от линзы до изображения f , фокусное расстояние линзы F , расстояние от предмета до переднего главного фокуса α , расстояние от заднего главного фокуса до изображения α' , высота предмета h, высота его изображения h' .

Из рисунка 153 видно, что ΔABC ~ ΔCLO, ΔA'B'C'' ~ ΔKOC'' , ΔABO ~ ΔA'B'O. Из подобия треугольников следует

	;	(1)
	;	(2)
	;	(3)

Используя соотношения (1) и (2), получим:

αα’=F²

(4)

С учетом того, что d = α + F, f = α′ + F (см. рис. 153), находим α = d - F и α′ = f - F и подставляем в формулу (4):

(d - F)(f - F) = df - Ff - dF+ F² = F²

Откуда получаем df = Ff + dF.

Разделив обе части последнего выражения на dfF, получаем формулу тонкой линзы:

(5)

Для практического использования формулы линзы следует твердо запомнить правило знаков:

Для собирающей линзы, действительного источника и действительного изображения величины F, d, f считают положительными. Для рассеивающей линзы, мнимого источника и мнимого изображения — F, d, f считают отрицательными.

Заметим, что предмет или источник является мнимым только в том случае, если на линзу падает пучок сходящихся лучей.

Таким образом, линза с F > 0 является собирающей (положительной), а с F < 0 — рассеивающей (отрицательной).

Линейным (поперечным) увеличением Г называется отношение линейного размера изображения h' к линейному размеру предмета h. Из соотношения (3) находим линейное увеличение тонкой линзы

(6)

В современных оптических приборах для улучшения качества изображений используются системы линз. Оптическая сила D системы тонких линз, сложенных вместе, равна сумме их оптических сил D_i

D = D₁ + D₂ + ... + D_n

(7)