§ 7. Паняцце дапаможнага алгарытму

7.6. Рэкурсія

Рэкурсія — у праграмаванні выклік падпраграмы (прама ці ўскосна) з яе ж самой. Колькасць укладзеных выклікаў падпраграмы называюць глыбінёй рэкурсіі.

Адрозніваюць прамую (простую, непасрэдную) і ўскосную (складаную, апасродкаваную) рэкурсію.

Прамая рэкурсія: пры апісанні функцыі выкарыстоўваецца зварот да яе ж самой, але з іншым наборам параметраў.

Ускосная рэкурсія: падпраграма выклікае якую-небудзь іншую падпраграму, у апісанні якой змяшчааецца выклік зыходнай (напрыклад, функцыя A выклікае функцыю B, а функцыя B выклікае функцыю A). Ускосны выклік можа быць арганізаваны і больш складаным чынам, г. зн. у рэкурсію могуць быць уключаны некалькі падпраграм.

Рэкурсіўная праграма дазваляе апісаць паўтаральныя дзеянні без відавочных паўтораў частак праграмы і выкарыстання цыклаў.

Структура рэкурсіўнай функцыі змяшчае каманду галінавання. Умова ў гэтай камандзе вызначае, калі рэкурсія павінна спыніцца. Па адной з галін гэтай каманды павінен адбывацца хоць бы адзін рэкурсіўны выклік (прамы ці ўскосны) функцыяй самой сябе. Правільна напісаная рэкурсіўная функцыя павінна гарантаваць, што праз канечную колькасць рэкурсіўных выклікаў будзе дасягнута выкананне ўмовы спынення рэкурсіі, у выніку чаго ланцуг паслядоўных рэкурсіўных выклікаў перапыніцца і выканаецца вяртанне.

Любая рэкурсіўная функцыя можа быць рэалізавана не рэкурсіўна.

Прыклад 7.14. Апісаць алгарытм Эўкліда з дапамогай рэкурсіўнай функцыі.

Этапы выканання задання

I. Зыходныя даныя: два лікі a, b.

II. Вынік: НОД (a, b).

III. Алгарытм рашэння задачы.

1. Увод зыходных даных.
2. Умовай спынення рэкурсіі будзе роўнасць лікаў. Калі лікі не роўныя, то выклікаем саму функцыю gcd. Пры гэтым адзін з параметраў замяняем на рознасць.
3. Вывад выніку.

IV. Апісанне пераменных: a, b, c, d — int.

Прыклад 7.15. Напісаць праграму, якая выводзіць раскладанне ліку на простыя множнікі.

Этапы выканання задання

I. Зыходныя даныя: число n.

II. Вынік: простыя множнікі ліку a.

III. Алгарытм рашэння задачы.

1. Увод зыходных даных.
2. Для атрымання раскладання лік трэба па чарзе спрабаваць дзяліць на простыя лікі: 2, 3, 5... . Калі падзяліўся, то дадзены лік уваходзіць у раскладанне і трэба паспрабаваць падзяліць на яго атрыманую дзель, калі не, то паспрабуем дзяліць на наступны просты. Працэс заканчваецца, калі ў дзелі атрымліваем 1.
3. Апішам рэкурсіўную функцыю razlog(a, b).

3.1. Параметр а — лік, які спрабуем дзяліць, параметр b — лік, на які спрабуем дзяліць.
3.2. Умова спынення рэкурсіі — параметр a роўны 1.
3.3. . Калі a дзеліцца на b, то пры выкліку функцыі першы параметр замяняем дзеллю a / b, калі не, то другі параметр павялічваем на 1.
3.4. Пры такой арганізацыі вылічэнняў можна не правяраць, што бягучы дзельнік з’яўляецца простым лікам, паколькі ні на адно састаўное бягучае значэнне першага параметру падзяліцца не зможа.
3.5. Вывад выніку будзе ажыццяўляцца пры звяртанні з рэкурсіі.

IV. Апісанне пераменных: n — int.

З дапамогай рэкурсіі зручна рэалізоўваць рашэнне такіх задач, у якіх сам алгарытм, што рэалізоўваецца, у сутнасці рэкурсіўны. Дастаткова проста апісаць рэкурсіўную функцыю, калі рашэнне задачы можа быць апісана з дапамогай рэкурэнтных суадносін.

Прыклад 7.16. Па азначэнні . Гэта значыць для таго, каб знайсці значэнне aⁿ неабходна выканаць n – 1 множянняў. Алгарытм хуткага (бінарнага) узвядзення ў ступень дазваляе скараціць колькасць множанняў. Алгарытм (для n ≥ 0) можа быць апісаны з дапамогай наступных рэкурэнтных суадносін:

$a to the power of n space equals space open curly brackets table attributes columnalign left end attributes row cell 1 comma space a space equals space 0 end cell row cell open parentheses a to the power of n over 2 end exponent close parentheses squared comma space space space a space space long dash space цотнае end cell row cell a space space asterisk times space a to the power of n space – space 1 end exponent comma space space n space long dash space няцотнае end cell end table close$

Напісаць праграму, якая знаходзіць aⁿ, выкарыстоўваючы апісаны вышэй алгарытм.

Этапы выканання задання

I. Зыходныя даныя: числа a і n.

II. Вынік: значэнне aⁿ.

III. Алгарытм рашэння задачы.

1. Увод зыходных даных.
2. Апішам рэкурсіўную функцыю binpow(x, k).

2.1. Параметр x — аснова ступені, параметр k — паказчык.
2.2. Умова спынення рэкурсіі — параметр k роўна 0. Функцыя павінна вярнуць 1.
2.3. Калі k — цотны, то пры выкліку функцыі другі параметр памяншаем у 2 разы, калі няцотны, то другі параметр памяншаем на 1.

3. Вывад выніку.

IV. Апісанне пераменных: a, n — int.

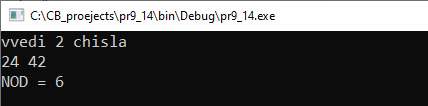
У некаторых дэкларатыўных або чыста функцыянальных мовах (такіх як Пралог ці Haskell) няма сінтаксічных сродкаў для арганізацыі цыклаў. У іх рэкурсія з’яўляецца адзіным даступным механізмам для арганізацыі паўтаральных вылічэнняў.

Пытанне пра пажаданасць выкарыстання рэкурсіўных функцый у праграміраванні неадназначны: з аднаго боку, рэкурсіўная форма можа быць структурна больш простай і нагляднай, асабліва калі сам рэалізуемы алгарытм у сутнасці рэкурсіўны. З іншага боку, звычайна рэкамендуецца пазбягаць рэкурсіўных праграм, якія прыводзяць (ці ў некаторых умовах могуць прыводзіць) да занадта вялікай глыбіні рэкурсіі.

Класічным прыкладам бясконцай рэкурсіі з’яўляюцца два пастаўленыя адно насупраць аднаго люстэркі: у іх утвараюцца два калідоры з адлюстраванняў люстэркаў, якія памяншаюцца.

Рэкурсія ляжыць у аснове пабудовы фрактальных малюнкаў.

Прыклад 7.14.

V. Праграма:

#include <iostream>

using namespace std;

int gcd (int x, int y)

{

if (x == y)

return x;

else

if (x > y)

gcd(x - y, y);

else

gcd(x, y - x);

}

int main()

{

int a, b;

cout << "vvedi 2 chisla" << endl;

cin >> a >> b;

int d = gcd(a, b);

cout << "NOD = " << d << endl;

return 0;

}

VI. Тэсціраванне:

Рэкурсіўная функцыя для вылічэння НАД двух лікаў можа быць запісана з выкарыстаннем тэрнарнай (ад лац. ternarius — трайны) умоўнай аперацыі.

int gcd (int a, int b)

{

return b ? gcd (b, a % b) : a;

}

Аперацыя, якая структурна запісваецца як o1 : o2 : o3, вяртае свой другі (o2) або трэці (o3) аперанд у залежнасці ад значэння лагічнага зададзенага выразу, зададзенага першым аперандам (o1).

Прыклад 7.15.

V. Праграма:

#include <iostream>

using namespace std;

void razlog (int a, int b)

{

if (a > 1)

if ( a % b == 0){

razlog(a / b, b);

cout << b << " ";

}

else

razlog(a, b + 1);

}

int main()

{

int n;

cout << "n = ";

cin >> n;

razlog(n, 2);

return 0;

}

VI. Тэсціраванне:

VII. Аналіз выніку.

Каб зразумець, чаму мы перабіраем простыя множнікі, пачынаючы з меншага, а праграма выводзіць іх у адваротным парадку, распішам парадак выканання каманд у праграме.

№	a	b	Каментарыі
1	60	2	a > 1, 60 % 2 = 0, выклік (60 / 2, 2), пасля выкліку ёсць каманда вываду
2	30	2	a > 1, 30 % 2 = 0, выклік (30 / 2, 2), пасля выкліку ёсць каманда вываду
3	15	2	a > 1, 15 % 2 ≠ 0, выклік (15, 3) пасля выкліку няма каманд
4	15	3	a > 1, 15 % 3 = 0, выклік (15 / 3, 3), пасля выкліку ёсць каманда вываду
5	5	3	a > 1, 5 % 3 ≠ 0, выклік (5, 4), пасля выкліку няма каманд
6	5	4	a > 1, 5 % 4 ≠ 0, выклік (5, 5), пасля выкліку няма каманд
7	5	5	a > 1, 5 % 5 = 0, выклік (5 / 5, 5), пасля выкліку ёсць каманда вываду
8	1	5	умова a > 1 не выконваецца; пры гэтым выкліку функцыя скончыла работу, аднак не скончана работа пры тых выкліках, пасля якіх ёсць вывад.
9	5	5	вывад b = 5
10	15	3	вывад b = 3
11	30	2	вывад b = 2
12	60	2	вывад b = 2

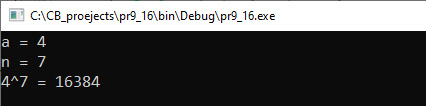
СЗахаванне выклікаў рэкурсіўнай функцыі разам са значэннямі параметраў і адрасам звяртання забяспечвае механізм стэка [1] выклікаў. Кожны рэкурсіўны выклік патрабуе некаторай колькасці аператыўнай памяці кампутара, таму пры празмеру вялікай глыбіні рэкурсіі можа наступіць перапаўненне стэка выклікаў.

Прыклад 7.16.

V. Праграма:

#include <iostream>

using namespace std;

int binpow(int x, int k)

{

if (k == 0)

return 1;

if (k % 2 == 1)

return binpow(x, k-1) * x;

else {

int b = binpow(x, k / 2);

return b * b;

}

int main()

{

int a, n;

cout << "a = ";

cin >> a;

cout << "n = ";

cin >> n;

cout << a << "^" << n << " = ";

cout << binpow(a, n) << endl;

return 0;

}

VI. Тэсціраванне:

[1] З паняццем стэка вы пазнаёміцеся пазней.