§ 12. Прямоугольное проецирование на две плоскости проекций. Метод Монжа

Прямоугольное проецирование на две плоскости проекций. Метод Монжа

Одна проекция не всегда однозначно определяет форму изображаемого предмета. Различные по форме предметы могут образовывать одинаковые проекции (см. рис. вверху справа).

Проецирование на две плоскости проекций. Для того чтобы получить представление о форме объемного предмета, проецирование выполняют на две плоскости проекций: горизонтальную Н и фронтальную V (рис. 42).
Плоскости проекций Н и V в пространстве размещают под прямым углом друг к другу. Линию пересечения этих плоскостей (ее обозначают х) называют осью проекций

Чтобы получить чертеж предмета на плоскости, обе плоскости Н и V совмещают в одну. Для этого горизонтальную плоскость проекций поворачивают на угол 90° так, чтобы она совпала с фронтальной плоскостью проекций. Плоскости проекций пересекаются осью проекций х (рис. 43, а).

Помните! При построении чертежа горизонтальную проекцию предмета Н всегда располагают под фронтальной V (рис. 43, б). Соединяют эти проекции линиями проекционной связи, которые являются проекциями проецирующих лучей.

Определите, какая проекция предмета является горизонтальной, а какая фронтальной. Свой ответ объясните.

Прямоугольное проецирование еще называют ортогональным. Основоположником ортогонального проецирования считается французский ученый Гаспар Монж (рис. 44). Метод Монжа — это метод прямоугольного проецирования на две взаимно перпендикулярные плоскости проекций. Линия пересечения двух плоскостей проекций называется осью проекций. Получаемые при этом ортогональные проекции, помещенные в одну плоскость, образуют комплексный чертеж, или эпюр Монжа.
Гаспар Монж положил начало развитию науки «Начертательная геометрия». Изложенный Монжем метод ортогонального проецирования на две взаимно перпендикулярные плоскости проекций был и остается основным методом составления технических чертежей.
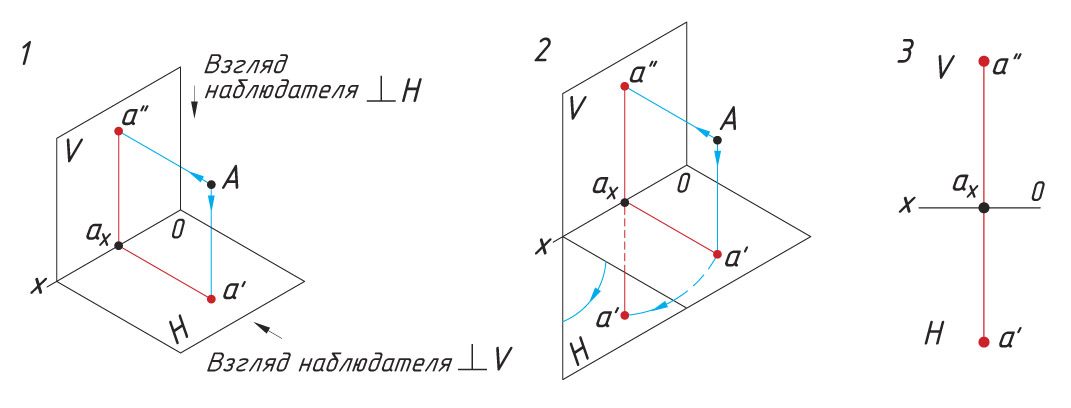
Построение двухпроекционного чертежа точки. Рассмотрим пример построения двухпроекционного чертежа точки (см. Памятку 6).

Памятка 6. Алгоритм построения двухпроекционного комплексного чертежа детали
Для того чтобы облегчить понимание последовательности проецирования на две плоскости проекций, построение двухпроекционного чертежа детали будет показано на бумаге в клетку
Сначала выполняется проецирование детали на фронтальную плоскость V. На наглядном изображении эта грань окрашена в голубой цвет 1. В соответствии с размерами проводятся вспомогательные линии 2. Сплошной основной толстой линией обозначается контур детали
3. Чтобы проекции находились одна под другой, проводятся линии проекционной связи, перпендикулярные к оси х, и определяется длина детали
4. Затем выполняется проецирование детали на фронтальную плоскость Н (светло-голубая плоская и голубая наклонная грани). Они имеют одинаковую ширину. Ширина детали 15 мм, ее ограничивают по бокам две грани голубого цвета, которые при взгляде сверху будут проецироваться в прямую линию
5. Если посмотреть сверху на деталь, то можно увидеть две грани под углом (голубую и светло-голубую), которые разделяет линия. Опускается соответствующая линия проекционной связи с фронтальной проекции на горизонтальную 6. Обводятся контуры детали сплошной основной толстой линией 7. Наносится осевая линия и проставляются размеры детали

1. Из точки А на плоскости V и H опускают перпендикуляры и получают проекции точки А: а′ — горизонтальная проекция и а″ — фронтальная проекция.
2. Мысленно удаляют точку А и поворачивают плоскость Н вокруг оси Ох на угол 90° вниз до совмещения с плоскостью V.
3. Проекции а′ и а″ расположились на одной прямой а′а″. Линия а′а″ называется линией проекционной связи.

Помните! Фронтальная и горизонтальная проекции точки всегда находятся на перпендикуляре к оси проекций ох.
Отрезок а′ах — расстояние точки А до плоскости V. Отрезок а″ах — расстояние точки А до плоскости Н.

Основы начертательной геометрии возникли еще в глубокой древности. Греческий геометр Евклид и римский архитектор Витрувий внесли большой вклад в развитие методов построения изображений пространственных форм на плоскости. Бурное развитие архитектуры, живописи и скульптуры в эпоху Возрождения создало условия для развития методов построения изображений пространственных форм на плоскости. В это время вводится целый ряд основных понятий: центральное проецирование, картинная плоскость, дистанция, главная точка, линия горизонта, дистанционные точки и т. д. Одним из первых, кто применял перспективу в своих работах, был итальянский архитектор и ученый Ф. Брунеллески. В трактате по перспективе Леонардо да Винчи приводятся примеры применения перспективных изображений, сведения о воздушной и линейной перспективе и теории светотени. Большой вклад в теорию перспективы внесли Альбрехт Дюрер, Гвидо Убальди, Жерар Дезарг. Но только в 1798 г. французский инженер и ученый Гаспар Монж сформулировал главные элементы теории построения графических изображений.