§ 10. Способы построения сопряжения

Способы построения сопряжений

Рассмотрим построение сопряжений различных типов.
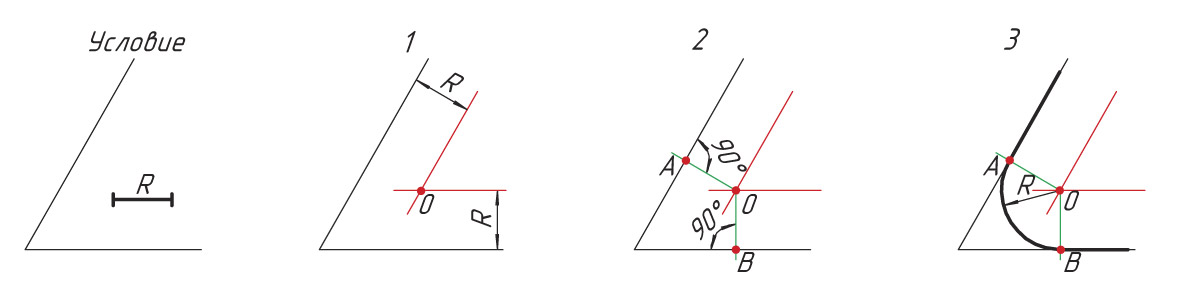
Построение сопряжения угла или двух прямых дугой заданного радиуса

Последовательность построения

1. Проводят вспомогательные прямые параллельно заданным, удаленные на расстоянии, равном заданному радиусу R. На пересечении вспомогательных прямых отмечают центр сопряжения О.
2. Из центра сопряжения О опускают перпендикуляры к прямым. Получают точки сопряжения А и В.
3. Из точки О проводят дугу сопряжения заданным радиусом R, соединяя точки сопряжения А и В.

Как вы считаете, есть ли различия в построении сопряжений острого и тупого угла? Ответ обоснуйте.

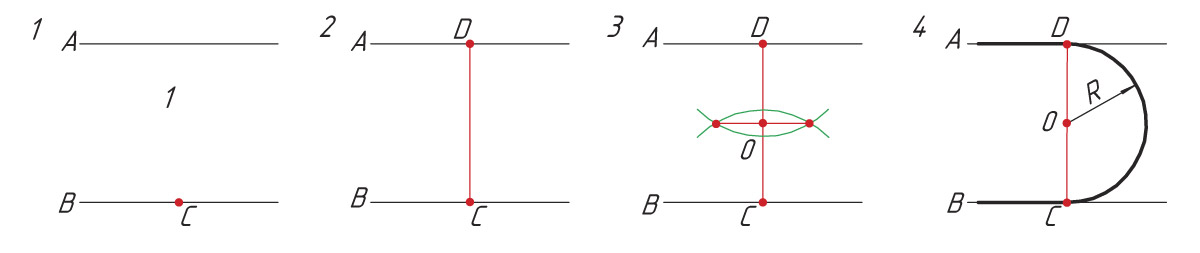
Построение сопряжения двух параллельных прямых
Последовательность построения
1. На прямой В берут произвольную точку С.
2. В точке С восстанавливают перпендикуляр до пересечения его с прямой А в точке D.
3. Разделив отрезок DC пополам, находят центр сопряжения О.
4. Из центра сопряжения О радиусом сопряжения R = OD = OC проводят дугу, соединяя точки сопряжения D и С.

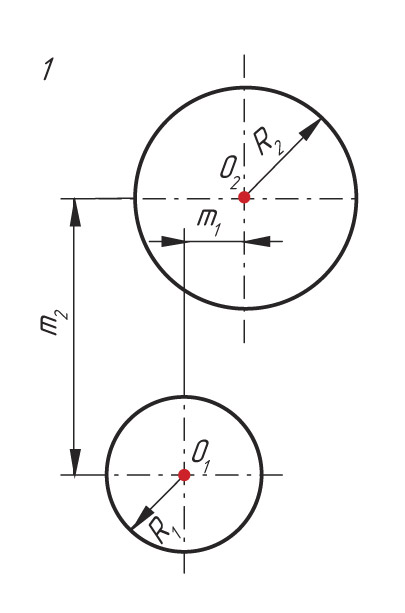
Построение сопряжения прямой и окружности

Последовательность построения
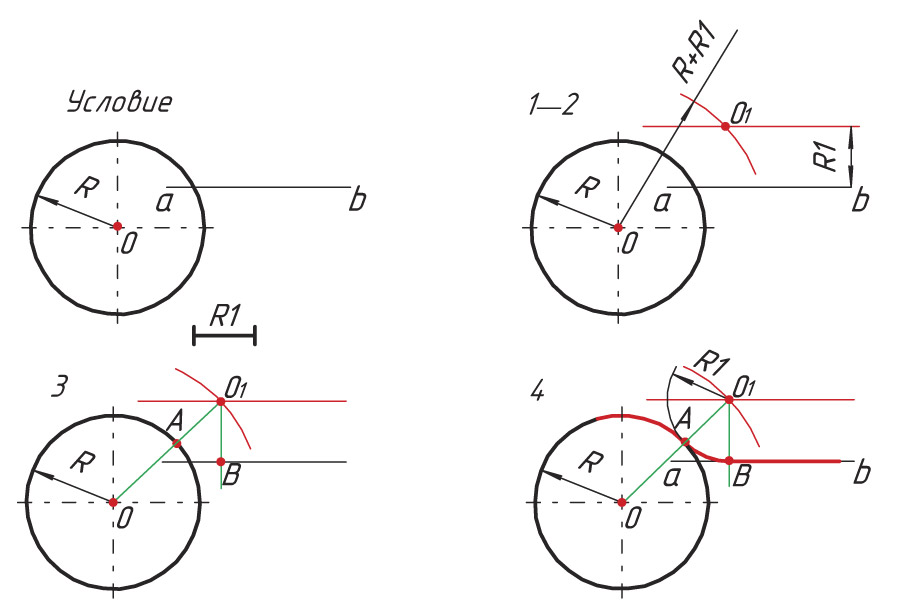
1. Проводят вспомогательную прямую, параллельную прямой а и удаленную от нее на расстоянии R₁.
2. Из центра окружности О проводят вспомогательную дугу радиусом, равным сумме радиусов окружности R и дуги сопряжения R₁, до пересечения в точке О₁.
3. Из точки О₁ опускают перпендикуляр до пересечения его с прямой аb в точке В. Соединяют точки О и О₁. Находят точку сопряжения А.
4. Из центра сопряжения О₁ радиусом сопряжения R₁ проводят дугу сопряжения, соединив точки сопряжения А и В.

Помните! Сначала сплошной толстой основной линией обводят дугу сопряжения, затем — дугу окружности и прямую.

Используя рисунок, расскажите, как выполнить сопряжение окружности и прямой линии.

Построение касательной к окружности из заданной точки.
1. Соединяют точку А с центром окружности О.
Полученный отрезок ОА делят пополам и получают точку О₁.
2. Из точки О₁ радиусом R равным О₁А строят вспомогательную окружность. Точка пересечения вспомогательной окружности и заданной окружности В является точкой сопряжения.
3. Соединив точки В и А, получим касательную к окружности.

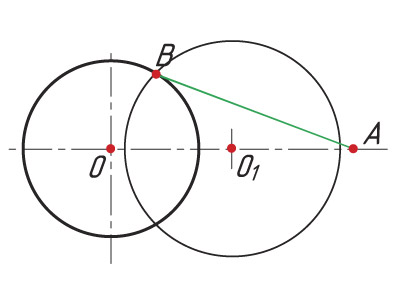
Построение сопряжения двух окружностей
Сопряжение двух окружностей осуществляется по внутреннему и внешнему контурам или может быть смешанным (см. Памятку 5)

Памятка 5. Построение сопряжений
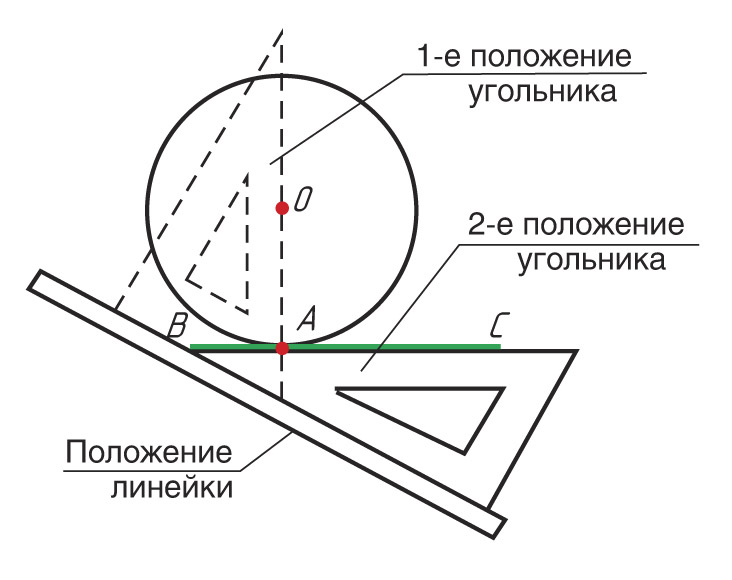
Построение касательной к окружности без использования дуг с помощью угольника и линейки
Построение смешанного сопряжения

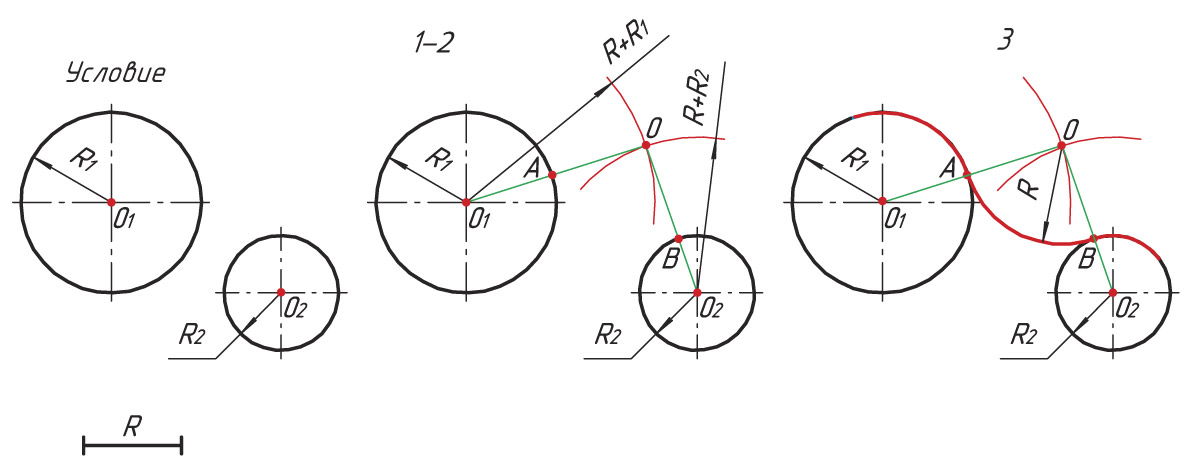
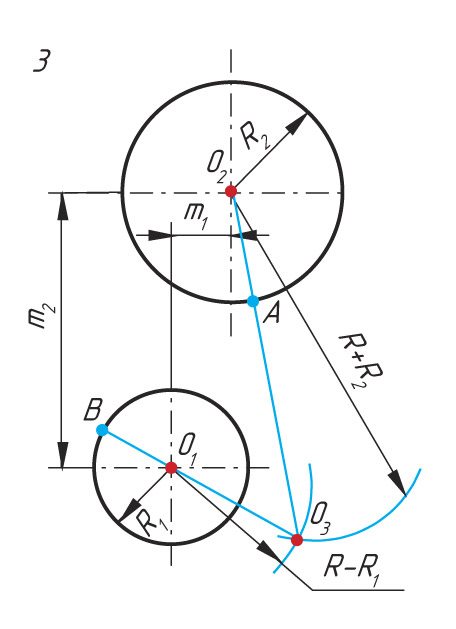
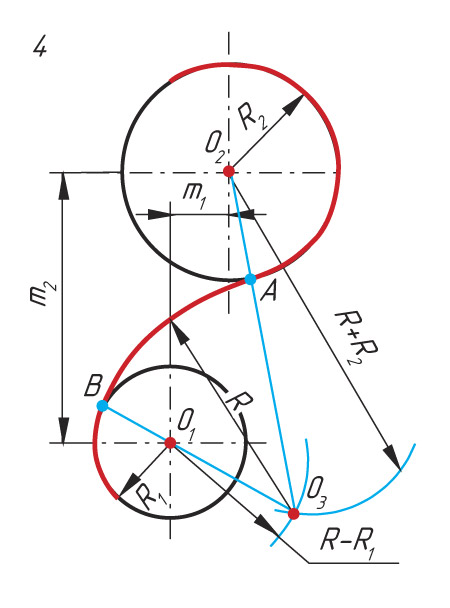
Рассмотрим примеры сопряжения двух окружностей с радиусами R1 и R2 дугой радиусом R.

Последовательность построения сопряжения по внешнему контуру

1. Из центра окружностей О₁ и О2 проводят вспомогательные дуги радиусом, равным сумме радиусов окружностей R + R₁ и R + R₂.
2. Точку пересечения вспомогательных дуг О соединяют с центром окружностей О₁ и О₂. Находят точки сопряжения А и В.
3. От центра сопряжения О радиусом сопряжения R проводят дугу сопряжения, соединив точки А и В.

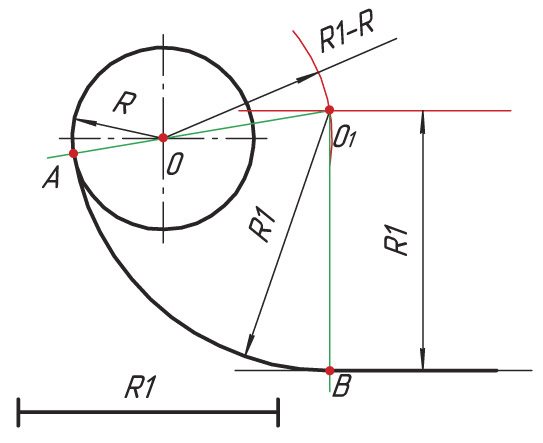
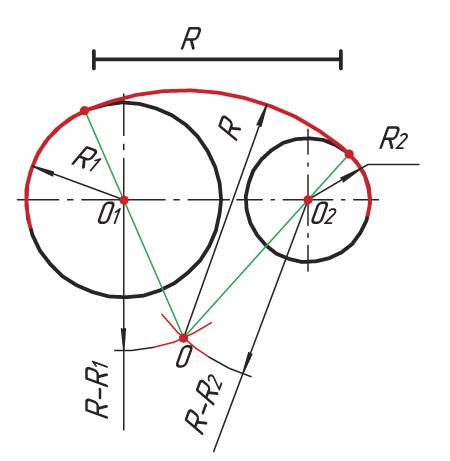
Последовательность построения сопряжения по внутреннему контуру

Построение сопряжения двух окружностей по внутреннему контуру схоже с построением сопряжения по внешнему контуру. Разница состоит лишь в том, что из центров окружностей О₁ и О₂ проводят вспомогательные дуги радиусом, равным разности радиусов окружностей R − R₁ и R − R₂.

Используя данный рисунок, составьте алгоритм построения сопряжения двух окружностей по внутреннему контуру.

Сегодня сложно представить, что когда-то люди рисовали, чертили и создавали шедевры без помощи графических редакторов и программ для моделирования. Именно поэтому работы современного художника из Венесуэлы Рафаэля Араужо кажутся особенно интересными. Мастер без помощи компьютера и современных технологий создает чертежи и расчеты полета бабочек или раковины моллюска наутилуса с помощью циркуля, лекала, линейки и карандаша, используя геометрические построения на основе принципа золотого сечения.