§ 19. Бинарный поиск в отсортированном массиве

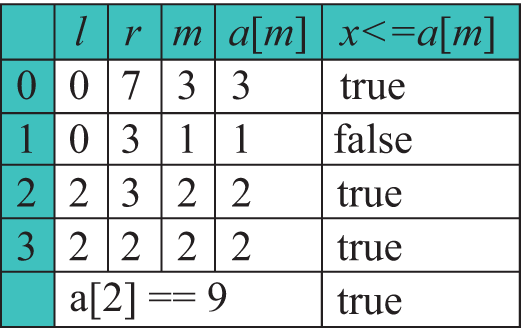
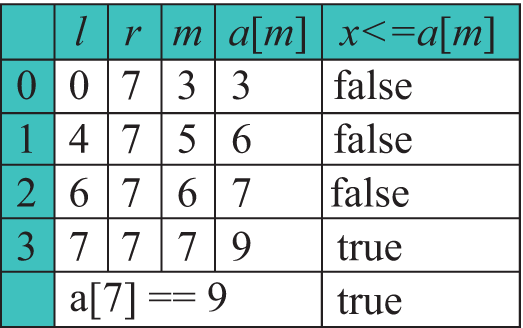
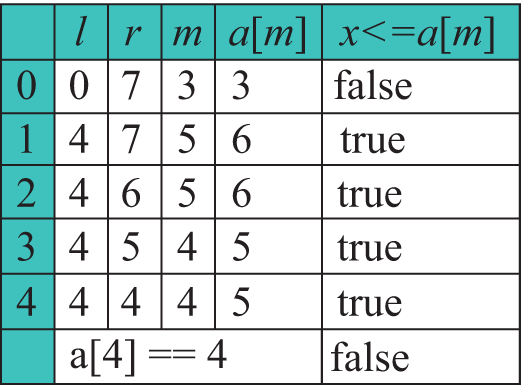
В предыдущем параграфе говорилось о том, что в отсортированном массиве поиск элемента можно осуществлять, не просматривая весь массив.

Для того чтобы понять, как это можно сделать, рассмотрим следующую задачу. Предположим, что кто-то загадал целое число от 1 до 100. Чтобы отгадать число, можно задавать вопросы, ответом на который будет «да» или «нет». Один из вариантов отгадывания — это задавать вопросы вида «Это 1?», «Это 2?» и т. д. В самом худшем случае придется задать 99 вопросов. Это стратегия линейного (последовательного) поиска. Здесь мы не учитываем тот факт, что числа от 1 до 100 расположены в порядке возрастания. Если задать вопрос «Это число больше 50?», то при ответе «да» станет понятно, что среди первых 50 чисел загаданного числа нет и его нужно угадывать среди чисел от 50 до 100. Если ответ «нет», то из рассмотрения исключаются числа, которые больше 50. В любом случае количество возможных чисел сокращается в два раза. Дальше, в зависимости от ответа, спрашиваем: «Это число больше 75 (25)?» и сокращаем область просмотра еще в два раза. Для следующего вопроса выбираем число, стоящее в середине оставшегося промежутка чисел.

Таким образом, какое бы число (от 1 до 100) ни было загадано, угадать его можно не более чем за 7 вопросов (2⁷ = 128 > 100), что существенно меньше, чем 99 (результат линейного поиска).

Такой метод поиска называется бинарным поиском. Встречаются и другие названия этого метода: двоичный поиск, логарифмический поиск, метод деления пополам, дихотомия.

В программировании такой поиск применяют для нахождения элемента x в отсортированном массиве. Поиск элемента в массиве
а = {0, 1, 2, 3, 5, 6, 7, 9} показан в примере 19.1.

Формальное описание алгоритма:

1. Определяем левую и правую границы промежутка поиска (вначале l = 0, r = n - 1).

2. Искомый элемент сравнивается с элементом массива, стоящим посередине (m = (l + r) / 2):

• если значение искомого элемента не больше среднего элемента, то исходной последовательностью считается массив
  от 0 до r = m (изменяется правая граница);
• если значение искомого элемента больше среднего элемента, то исходной последовательностью считается массив
  от l = m +1 до n – 1 (изменяется левая граница.

3. Для новой последовательности этот процесс повторяется.

4. Продолжаем деление промежутка поиска пополам до тех пор, пока левая граница поиска меньше правой.

Есть два способа реализации этого алгоритма: итеративный (пример 19.2) и рекурсивный (пример 19.3). Функция возвращает значение true, если элемент найден, и false в противном случае.

Если необходимо знать еще и место, на котором находится искомый элемент, то возможны два варианта. В качестве возвращаемого значения функции определить структуру с двумя полями (bool и int). Логическое поле будет служить для определения того, найден элемент или нет, а целочисленное будет хранить индекс найденного элемента. В случае если элемент не найден, то значение второго поля будет определять место для вставки элемента в массив без нарушения упорядоченности массива (пример 19.4).

Другим возможным вариантом для сохранения индекса найденного элемента может стать дополнительный параметр, значение которого будет передаваться по ссылке.

Для оценки количества операций, необходимых для получения результата, будем рассуждать следующим образом. Пусть натуральное k — количество операций сравнения, которые необходимы для нахождения элемента в упорядоченном массиве методом дихотомии. Тогда число k определяется из следующего неравенства: n ≤ 2^k, причем k — минимальное из всех возможных.

Пример 19.5. Дан линейный отсортированный массив целых чисел. Написать программу, которая получит количество элементов, расположенных между x и y. (Предполагается, что такие элементы существуют и единственны.) Массив упорядочен в порядке убывания. Данные прочитать из файла. Числа x и y ввести с клавиатуры.

Этапы выполнения задания

I.Исходные данные: переменные n -количество чисел в массиве, a — массив, числа x и y.

II. Результат: количество элементов между x и y.

III. Алгоритм решения задачи.

1. Ввод исходных данных.
2. Для решения задачи будем использовать алгоритм бинарного поиска. Согласно условию задачи массив отсортирован по убыванию, поэтому в программе необходимо поменять знак сравнения: «<=» на «>=» при сравнении искомого элемента со средним.
3. Определим позицию чисел x и y в массиве.
4. Ответом будет значение, равное модулю разности позиций для чисел x и y минус 1.
5. Вывод результата.

IV. Описание переменных: n, x, y – int, a –  vector<int>.